Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 95

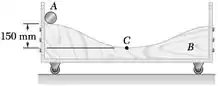
Um cilindro A de aço de 3 kg e um carrinho B de madeira de 5 kg estão em repouso na posição mostrada na figura quando o cilindro recebe um empurrãozinho, fazendo com que ele role sem deslizar ao longo da superfície superior do carrinho. Desprezando o atrito entre o carrinho e o chão, determine a velocidade do carrinho quando o cilindro passa pelo ponto mais baixo da superfície em C.

Passo 1

O enunciado pede que a gente determine a velocidade do carrinho quando o cilindro passa pelo ponto mais baixo da superfície em C.

Cinemática (quando o cilindro está passando de C)

← + v B = v C = r ω - v - A

ω = v - A + v B r

Passo 2

Componentes → +   x :

m A v - A - m B v B = 0

6   lb g v - A = 10   lb g v B ;               v B = 0.6 v - A

Trabalho:

U 1 → 2 = W A 6   in. = 6   lb 6 12 ft = 3   ft ∙ lb ;               T 1 = 0

Energia cinética:

T 2 = 1 2 m A v - A 2 + 1 2 I - ω 2 + 1 2 m B v 3 2

v B = 0.6 v - A ;               ω = v - A + v 0 r = v A + 0.6 v A r = 1.6 v A r

T 2 = 1 2 6   lb g v - A 2 + 1 2 1 2 6   lb g r 2 1.6 v A r 2 + 1 2 10   lb g 0.6 v A 2

= 3 g v - A 2 + 3.84 g v - A 2 + 1.5 g v - A 2 = 12.48 g v - A 2

Passo 3

Princípio de trabalho e energia.

T 1 + U 1 → 2 = T 2

0 + 3   ft ∙ lb = 8.64 22.2 v A 2

v - A 2 = 11.181               v - A = 3.344   ft/s →

v B = 0.6 v - A = 0.6 3.344

Resposta

v B = 2.01   ft/s ←

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cursor C de 3 kg é preso a uma mola e pode deslizar na barra AB, podendo girar em torno do plano horizontal. O momento de inércia da massa da barra AB em relação a extremidade A é 0,5 kg ∙ m2. A mo
O cursor C tem massa de 8 kg e pode deslizar livremente sobre a barra AB, que por sua vez pode girar livremente em um plano horizontal. O conjunto está girando com uma velocidade angular ω de 1,5 rad/
No Problema 17.89, determine a intensidade requerida da velocidade relativa inicial vr para que, durante o movimento subsequente, a distância mínima entre o cursor C e o ponto B seja de 300 mm.
Uma bala de 40 g é disparada com uma velocidade horizontal de 550 m/s contra a extremidade inferior de uma barra delgada de 7,5 kg e comprimento L = 800 mm. Sabendo que h = 300 mm e que a barra está i