Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 91

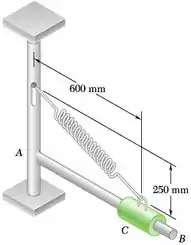
Um cursor C de 3 kg é preso a uma mola e pode deslizar na barra AB, podendo girar em torno do plano horizontal. O momento de inércia da massa da barra AB em relação a extremidade A é 0,5 kg ∙ m2. A mola tem uma constante k = 3.000 N/m e um comprimento indeformado de 250 mm. No instante mostrado na figura, a velocidade do cursor relativa à barra é zero e o conjunto está girando com uma velocidade angular de 12 rad/s. Desprezando o efeito do atrito, determine (a) a velocidade angular do conjunto quando o cursor passa pelo ponto localizado 180 mm da extremidade A da barra, (b) a velocidade correspondente do cursor em relação à barra.

Passo 1

O enunciado pede que a gente determine (a) a velocidade angular do conjunto quando o cursor passa pelo ponto localizado 180 mm da extremidade A da barra, (b) a velocidade correspondente do cursor em relação à barra.

Energia potencial da mola: comprimento indeformado = 10 pol.

Posição 1:

∆ = 26   in . - 10   in . = 16   in .

V 1 = 1 2 k ∆ 2 = 1 2 15   lb/in. 16   in. 2 = 1920   in ∙ lb

V 1 = 160   ft ∙ lb

Passo 2

Posição 2

∆ = 12.5   in . - 10   in . = 2.5   in .

V 1 = 1 2 k ∆ 2 = 1 2 15   lb/in. 2.5   in. 2 = 46.875   in ∙ lb

V 1 = 3.91   ft ∙ lb

Passo 3

Cinemática

Cinética: uma vez que os momentos de todas as forças sobre a mudança em A são zero, H A 1 = H A 2

I R ω 1 + m C v 0 r 1 = I R ω C + m C v 0 2 r 2

I R + m C r 1 2 ω 1 = I R + m C r 2 3 ω 2

Passo 4

Dados:

I R = 0.35   lb ∙ ft ∙ s 2 ,               m C = 6   lb 32.2

r 1 = 2   ft ,               r 2 = 7.5 12   ft ,               ω 1 = 12   rad/s

3.35   lb ∙ ft ∙ s 2 + 6   lb 32.2 2   ft 2 12   rad/s = 0.35   lb ∙ ft ∙ s 2 + 6   lb 32.2 7.5 13 b 2 ω 2

13.1441 = 0.42279 ω 2 ;               ω 2 = 31.089   rad/s

Passo 5

  1. Velocidade angular.

    2. Energia cinética.

    T 1 = 1 2 I A ω 1 2 + 1 2 m C v D 1 2 + 1 2 m C v R 1 2 = 1 2 0.35   lb ∙ ft ∙ s 2 12   rad/s 2 + 1 2 6   lb 32.2 2   ft 2 13   rad/s 2 + 0

    T 1 = 78.965   ft ∙ lb

    T 2 = 1 2 I R ω 2 2 + 1 2 m v B 2 2 + 1 2 m 2 v R 2 2 = 1 2 0.35     lb ∙ ft ∙ s 2 31.025   rad/s 2

    + 1 2 6   lb 32.2 25 12 ft 2 31.089   rad/s 2 + 1 2 6   lb 32.2 v R 2 2

    T 2 = 204.32 + 0.04317 v 2 2

    Passo 6

    Princípio de conservação de energia:

    T 1 + V 1 = T 2 + V 2

    Lembrando:

    V 1 = 160   ft ∙ lb               e                 V 2 = 3.91   ft ∙ lb

    78.865 + 160 = 204.32 + 0.09317 v r 2 2 + 3.91

    30.638 = 0.09317 v r 2 2

    Passo 7

  2. Velocidade do colar em relação à haste.

Resposta

b )   v r 2 = 18.13   ft/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma roda de raio r e raio centroidal de giração k é liberada do repouso a inclinação mostrada no tempo t = 0. Supondo que a roda rola sem deslizar, determine (a) a velocidade de seu centro no tempo t,
Dois cilindros uniformes, cada um com peso W = 14 lb e raio r = 5 pol., são conectados por uma correia, conforme mostrado. Sabendo que no instante mostrado a velocidade angular do cilindro A é de 30 r
Considere uma laje rígida inicialmente em repouso e submetida a uma força impulsiva F contida no plano da laje. Definimos o centro de percussão P como o ponto de intersecção da linha de ação de F com
O rotor de um motor elétrico tem uma velocidade angular de 3.600 rpm quando a carga e a potência são cortadas. O rotor de 50 kg, com um raio de giração centroidal de 180 mm, chega então ao estado de r
O rotor de um motor elétrico tem massa de 25 kg e raio de giração de 180 mm. Observa-se que são necessários 4,2 min para o rotor chegar ao repouso a partir de uma velocidade angular de 3.600 rpm após