Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 96

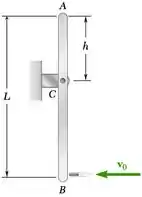
Uma bala de 40 g é disparada com uma velocidade horizontal de 550 m/s contra a extremidade inferior de uma barra delgada de 7,5 kg e comprimento L = 800 mm. Sabendo que h = 300 mm e que a barra está inicialmente em estado de repouso, determine (a) a velocidade angular da barra imediatamente após a bala se alojar nela, (b) a reação impulsiva em C, considerando que a bala se aloja em 0,001 s.

Passo 1

O enunciado pede que a gente determine (a) a velocidade angular da barra imediatamente após a bala se alojar nela, (b) a reação impulsiva em C, considerando que a bala se aloja em 0,001 s.

Barra:

L = 30   in. = 2.5   ft               m = 15 32.2 = 0.46584   lb ∙ s 2 /ft

I - = 1 12 m L 2 = 1 12 0.46584 2.5 2 = 0.24262   lb ∙ s 2 /ft

Passo 2

Bala:

m 0 = 0.08 32.2 = 0.0024845   lb ∙ s 2 /ft

Local de suporte:

h = 12   in. = 1.0   ft

Cinemática.

v B = L - h ω = 2.5 - 1.0 ω = 1.5 ω

v G = L 2 - h ω = 1.25 - 1.0 ω = 0.25 ω

Passo 3

Momentos sobre C:

m 0 v 0 L - h = m 0 v B L - h + m v 0 L 2 - h + I - ω

0.0024845 1800 1.5 = 0.0024845 1.5 ω + 0.46584 0.25 ω 0.25 + 0.24262 ω

Passo 4

  1. 6.7082 = 0.27546 ω                 ou                 ω = 25.249

    v B = 1.5 24.353 = 36.53   ft/s

    v G = 0.25 24.353 = 6.0881   ft/s

    Componentes horizontais → + :

    - m 0 v 0 + C Δ t = - m 0 v B - m v G :               C Δ t = m 0 v 0 - v B - m v 0

    C Δ t = 0.0024845 1800 - 36.53 - 0.46584 6.0881

    = 1.545   lb ∙ s

    Passo 2

C = C ∆ t ∆ t = 1.437 0.001

Resposta

a )   ω = 25.2   rad/s  

b )   C = 1545   lb →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de 3 kg e comprimento de 800 mm pode deslizar livremente no cilindro DE de 240 mm, que pode girar livremente no plano horizontal. Na posição mostrada na figura, o conjunto está girando com v
No helicóptero mostrado na figura, um rotor de cauda é usado para impedir a rotação da cabine à medida que a velocidade das pás principais é alterada. Admitindo que o rotor de cauda não esteja em oper
O disco B de 4 kg está ligado ao eixo de um motor montado sobre a placa A, que pode girar livremente em torno do eixo vertical C. A unidade motor-placa-eixo tem um momento de inércia de 0,20 kg ∙ m2 e
Uma plataforma circular A é presa a um aro de raio interno de 200 mm e pode girar livremente sobre um eixo vertical. É sabido que a unidade plataforma-aro tem massa de 5 kg e raio de giração de 175 mm
Um pequeno cursor C de 2 kg pode deslizar livremente sobre um anel fino de massa de 3 kg e raio de 250 mm. O anel está soldado a um eixo vertical curto, que pode girar livremente em um mancal fixo. In