Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 89

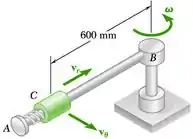
O cursor C tem massa de 8 kg e pode deslizar livremente sobre a barra AB, que por sua vez pode girar livremente em um plano horizontal. O conjunto está girando com uma velocidade angular ω de 1,5 rad/s quando uma mola localizada entre A e C é liberada, projetando o cursor ao longo da barra com uma velocidade relativa inicial vr = 1,5 m/s. Sabendo que o momento de inércia combinado da barra e da mola em relação a B é de 1,2 kg ∙ m2 , determine (a) a distância mínima entre o cursor e o ponto B no movimento subsequente, (b) a velocidade angular correspondente do conjunto.

Passo 1

O enunciado pede que a gente determine (a) a distância mínima entre o cursor e o ponto B no movimento subsequente, (b) a velocidade angular correspondente do conjunto.

v θ = r ω

Momentos da inércia.

I = I B + m C r 2 = 1.2 + 8 r 2

Passo 2

Conservação do momento angular.

H B 1 = H B 2 :                 I B ω 1 + m C v θ 1 r 1 = I B ω 2 + m C v θ 2 r 2

I B + m C r 1 2 ω 1 = I B + m C r 2 2 ω 2                 ou                 I 1 ω 1 = I 2 ω 2

ω 2 = I 1 ω 1 I 2

Energia potencial.

V 1 = 0               V 2 = 0

Passo 3

Energia cinética.

T = 1 2 m C v r 2 + 1 2 m C v θ 2 + 1 2 I B ω 2 = 1 2 m C v r 2 + 1 2 I ω 2

Posição 1. Só depois de mola seja liberada.

r = r 1

v r = v r 1

ω = ω 1

I = I 1

Passo 4

Posição 2. A distância r é mínima.

r = r 2

v r = v r = 0

ω = ω 2

I = I 2

Passo 5

Conservação de energia.

T 1 + V 1 = T 2 + V 2 :                 1 2 m C v r 1 2 + 1 2 I 1 ω 1 2 + 0 = 0 + 1 2 I 2 ω 2 2

m C v r 1 2 = I 2 I 1 ω 1 I 2 2 - I 1 ω 1 2

I 1 I 1 I 2 - 1 ω 1 2

Passo 6

Dados.

r 1 = 600   mm = 0.6   m

ω 1 = 15   rad/s

v r 1 = 1.5   m

I 1 = 1.2 + 8 0.6 2 = 4.08   kg ∙ m 2

Equação (2):

8 1.5 2 = 4.08 I 1 I 2 - 1 1.5 2

I 1 I 2 = 2.9608

I 2 = 4.08 2.9608 = 1.378 = 1.2 + 8 r 2 2

Passo 7

  1. r 2 = 0.14917   m

    Passo 8

  2. Equação (1):

ω 2 = 4.08 1.378 1.5

ω 2 = 4.44   rad/s

Resposta

a )   r 2 = 149.2   mm

b )   ω 2 = 4.44   rad/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro de 240 mm de raio e massa de 8 kg repousa sobre um transportador de 3 kg. O sistema está em estado de repouso quando uma força P de intensidade 10 N é aplicada como mostrado na figura dura
Um cilindro de 240 mm de raio e massa de 8 kg repousa sobre um transportador de 3 kg. O sistema está em estado de repouso quando uma força P de intensidade 10 N é aplicada como mostrado na figura dura
No arranjo das engrenagens mostrado na figura, as engrenagens A e C estão presas à barra ABC, que é livre para girar em torno de B, enquanto a engrenagem interna B é fixa. Sabendo que o sistema está e
Uma esfera de raio r e massa m é colocada sobre um piso horizontal sem velocidade linear, mas com velocidade angular ω 0 no sentido horário. Representando por μ k o coeficiente de atrito cinético entr
Uma esfera de raio r e massa m é lançada ao longo de uma superfície horizontal rugosa com as velocidades iniciais mostradas na figura. Para que a velocidade final da esfera seja nula, expresse (a) a i