Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 103

A bobina tem uma massa de 100 kg e um raio de giração k G = 0,3   m . Se os coeficientes de atrito cinético e estático em A são μ s = 0,2 e μ k = 0,15 , respectivamente, determine a aceleração angular da bobina se P = 50 N.

Passo 1

Começaremos o exercício calculando o momento de inércia da bobina em relação ao seu centro de massa:

I G = m k G 2 = 100 0,3 2 → I G = 9   k g . m 2

Passo 2

Iremos assumir que o rolo de grama não desliza, sendo assim:

a G = α r = α ( 0,4 )

Agora iremos aplicar as equações de movimento para o sistema com base no diagrama a seguir:

+ →   ∑ F x = m a G x

50 + F A = 100 a G

50 + F A = 100 0,4 α

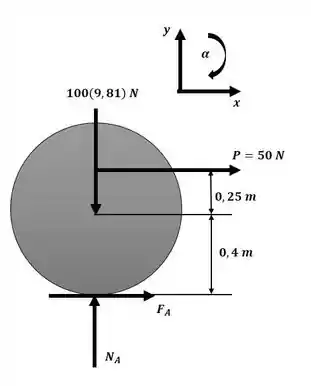
Essa será nossa equação 1.

+ ↑   ∑ F y = m a G y

N A - 100 9,81 = 0 → N A = 981   N

↻ +   ∑ M G = I G α

50 0,25 - F A 0,4 = 100 0,3 2 α → F A = 31,25 - 22,5 α

Essa será nossa equação 2.

Passo 3

Agora iremos substituir a equação 2 na 1:

50 + ( 31,25 - 22,5 α ) = 100 0,4 α

α = 1,3   r a d / s 2

Agora iremos substituir esse valor na equação 2:

F A = 31,25 - 22,5 ( 1,3 ) → F A = 2   N

Dessa forma, como F A m a x = μ s N A = 0,2 981 = 196,2   N > F A = 2   N , a bobina não desliza.

Resposta

α = 1,3   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia I z de massa do cone formado girando-se a área sombreada em torno do eixo z . A densidade do material é ρ . Expresse o resultado em termos da massa m do cone.
O cone circular reto é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do cone. O cone tem uma densidade c
O tronco de cone é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do tronco. O tronco tem uma densidade c
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia em relação ao eixo x e expresse o resultado em termos da massa total m do paraboloide. O materia
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o raio de giração k x . A densidade do material é ρ = 5 Mg/m3.