Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 19

O cilindro hidráulico mostrado na figura exerce uma força de 3 kN para a direita no ponto B e para a esquerda no ponto E. Determine a intensidade do binário M necessária para girar o tambor no sentido horário a uma velocidade constante.

Passo 1

Beleza! Vamos começar esse excercício desenhando o DCL do cilindro quando o cilindro está se movimentando com velocidade constante:

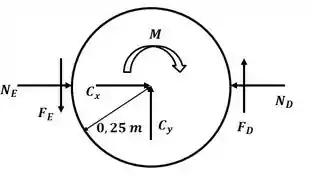
Dessa forma, como o cilindro está girando, temos as forças de atrito dinâmico dos dois lados, dadas por:

F E = μ k N E → F E = 0,3 N E

F D = μ k N D → F D = 0,3 N D

Agora vamos aplicar o somatório de momento em relação ao centro do cilindro:

+ ↻ ∑ M C = 0

M - 0,25 F E - 0,25 F D = 0 → M = 0,25 F E + F D

Passo 2

Agora vamos analisar o braço do lado esquerdo:

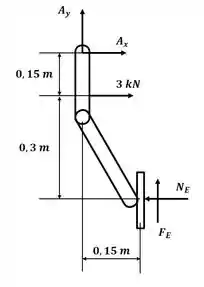
Aplicando o somatório de momento em relação ao ponto A, temos:

+ ↺ ∑ M A = 0

3 0,15 + F E 0,15 - N E 0,45 = 0 → 0,45 + 0,3 N E 0,15 - 0,45 N E = 0

N E = 1,11   k N

Dessa forma, substituindo o valor na fórmula para F E encontrada no passo 1:

F E = 0,3 N E = 0,3 1,11 → F E = 0,333   k N

Passo 3

Agora vamos analisar o braço do lado direito:

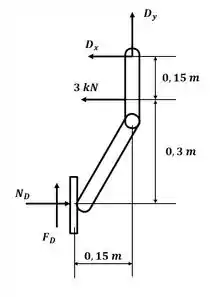
Aplicando o somatório de momento em relação ao ponto D, temos:

+ ↻ ∑ M D = 0

3 0,15 - F D 0,15 - N D 0,45 = 0 → 0,45 - 0,3 N D 0,15 - 0,45 N D = 0

N D = 0,91   k N

Dessa forma, substituindo o valor na fórmula para F D encontrada no passo 1:

F D = 0,3 N D = 0,3 0,91 → F D = 0,273   k N

Agora, substituindo os valores encontrados para F na equação do momento encontrada no passo 1, temos:

M = 0,25 F E + F D = 0,25 0,333 + 0,273 → M = 0,151   k N . m

Resposta

M = 0,151   k N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/43) As duas barras A C e B D são feitas do mesmo material . Determine o ângulo θ no qual a barra A C deslizará e faça um gráfico de θ em função do coeficiente de atrito estático μ s na faixa 0 ≤ μ s
6/37) O semicilindro homogêneo repousa sobre uma superfície horizontal e estásubmetido a uma força P aplicada a um cabo firmemente preso asua periferia . A força P é lentamente aumentada e mantida nor
6/39) A cabeça do grampo de marceneiro é soldada a seu eixo de diâmetro d e é projetada para prender a peça de trabalho A em seu lugar . O grampo é ajustado batendo inicialmente em sua cabeça com uma
6/40) A garra esquerda móvel de um sargento pode ser deslocada ao longo do conjunto para aumentar a capacidade de pegada do grampo . Para prevenir deslizamento da garra no trilho quando o grampo está
6/50) A embreagem de rotação em miniatura é projetada para permitir que o anel externo gire no sentido horário em relação ao eixo (hachurado) , mas impede rotação no sentido anti-horário . Isso é obti