Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 14
Resolva o Problema 8.13 considerando que o pacote B é colocado à direita dos pacotes A e C.
Passo 1
Tá legal! Para fazer esse exercício, vamos começar analisando os pacotes de trás pra frente, pois se o pacote que está atrás se mexer, os da frente também devem se mover, então, fazendo o DCL para o pacote B, temos:
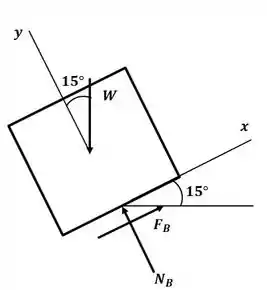
Então, vamos assumir que o bloco não se move e depois verificar se a força de atrito é suficiente para segurar ou não o bloco, então, aplicando o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora, calculando a força de atrito, temos:
Então, como temos o pacote B se moveria se estivesse sozinho.
Passo 2
Dessa forma, podemos analisar os três pacotes juntos, fazendo o DCL do sistema:
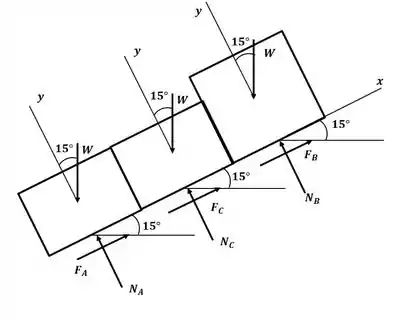
Como os pacotes possuem a mesma massa e estão sob o mesmo plano inclinado, temos:
Então, a força total que age sobre os blocos na direção é:
Agora, vamos calcular a força de atrito sobre os blocos, para o pacote B:
E, como o pacote A e C possuem o mesmo coeficiente de atrito, temos:
Então, a força de atrito total é:
Então como temos os três pacotes se movem.
Passo 3
Dessa forma, como os pacotes se movem, precisamos calcular a força de atrito cinética, para B, temos:
E, como A e C possuem os mesmos coeficientes de atrito, temos: