Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 23

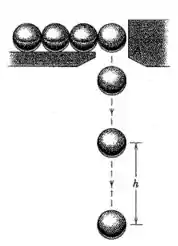
Pequenas bolas de aço caem do repouso através da abertura em a uma taxa constante de duas por segundo. Encontre a separação vertical de duas bolas consecutivas quando a mais baixa tiver caído metros. Despreze a resistência do ar.

Passo 1

Beleza, vamos dizer que é o instante em que a primeira bola cai pela abertura. Qual é a função que dá a altura que a bola percorre em função do tempo?

Como a bola parte do repouso, temos e podemos dizer que o ponto de onde elas caem é :

Vamos chamar essa função de , porque dá a altura percorrida pela primeira bola:

Se caem duas bolas a cada segundo (taxa constante), isso quer dizer que uma bola cai a cada segundos! Ou seja, a segunda bola vai cair no instante , e a função que da a altura dela é:

Passo 2

O que a questão quer saber é o seguinte: qual a diferença de altura entre as duas bolas quando :

Passo 3

Então só fica faltando encontrar quando

E então:

Pronto!

Resposta

A separação vertical é de .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Prob. 2/56, porém agora inclua os efeitos do arrasto aerodinâmico. As forças de arrasto provocam uma componente de aceleração em m / s 2 de 0,016 v 2 na direção oposta ao vetor velocidade, on

Uma bola é jogada verticalmente para cima com uma velocidade de 15 m/s. Determine o tempo do voo quando ela retorna para sua posição original.

Uma partícula move-se ao longo de uma linha reta com uma velocidade de v = 0,5 t 3 - 8 tm / s , onde t é dado em segundos. Determine a aceleração da partícula quando t = 2s .

Uma partícula move-se ao longo de uma linha reta de maneira que a sua aceleração é a = 4 t 2 - 2m / s 2 , onde t é dado em segundos. Quando t = 0 , a partícula está localizada 2 m à esquerda da origem

Inicialmente, o carro move-se ao longo de uma estrada reta com uma velocidade de 35 m/s. Se os freios são aplicados e a velocidade do carro é reduzida a 10 m/s em 15 s, determine a desaceleração const