Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 239
O foguete lançado verticalmente e o radar de rastreamento do Prob. 2/147 são apresentados aqui novamente. No instante em que , as medidas fornecem e , e a aceleração vertical do foguete é encontrada como . Para esse instante determine os valores de e .
Passo 1
Nosso objetivo é calcular e no instante em que . Existem duas direções importantes no movimento que nós precisamos definir:
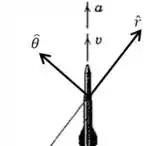
é o vetor unitário que aponta na direção em que cresce, e é o vetor unitário que aponta na direção em que o ângulo cresce.
O grande segredo dessa questão é perceber que o ângulo que o radar forma com a horizontal é igual ao ângulo entre e ! Dê uma olhada nesse desenho para entender porque isso acontece:
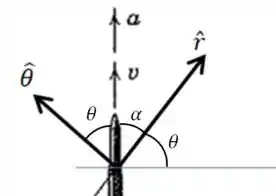
A partir daqui só temos que fazer algumas contas simples.
Passo 2
Vamos lembrar da expressão para o vetor velocidade em coordenadas polares:
E já que nós temos o ângulo entre e , podemos afirmar o seguinte:
E a outra componente da velocidade é:
Ok, agora vamos ver a aceleração.
Passo 3
Lembrando que e , podemos derivar a expressão da velocidade para achar a aceleração:
Beleza, agora (já que o vetor aceleração é paralelo à velocidade) vamos seguir o mesmo procedimento de antes:
E agora vamos substituir os valores numéricos que já temos:
Ótimo! A primeira equação dá o valor de e a segunda dá de . Resolvendo as duas vamos achar:
Resolvido!
Resposta
e .