Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 39

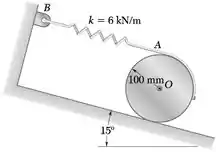
Um cilindro uniforme de 15 kg pode rolar sem deslizar em um plano inclinado de 15°. Uma esteira é presa ao aro do cilindro e uma mola mantém o cilindro em repouso na posição mostrada na figura. Se o centro do cilindro é movido 50 mm para baixo no plano inclinado e liberado, determine (a) o período de vibração, (b) a aceleração máxima do centro do cilindro.

Passo 1

O exercicio pede que a gente determine (a) o período de vibração, (b) a aceleração máxima do centro do cilindro.

Deflexão da mola.

x A = x 0 + x A / 0

x A / 0 = r θ

θ = x 0 r

x A = 2 x 0

F S = k x A + δ ST = k 2 x 0 + δ ST

  Σ M C = Σ M eff :             - 2 r k 2 x 0 + δ ST + r w sin ⁡ 15 ° = r m x ¨ 0 + I - θ ¨

Passo 2

Mas em equilíbrio,

x 0 = 0

Σ M C = 0 = - 2 r k δ ST + r w sin ⁡ 15 °

Passo 3

Substituindo a Eq. (2) na Eq. (1) e observando que

θ = x 0 r ,                 θ ¨ = x ¨ 0 r

r m x ¨ 0 + I - x ¨ 0 r + 4 r k x 0 = 0

I - = 1 2 m r 2

3 2 m r x ¨ 0 + 4 r k x 0 = 0

x ¨ 0 + 3 3 k m x 0 = 0

Passo 4

Frequência natural.

ω n = 8 3 k m = 8 30 × 12   lb/ft 3 30   lb 32.2   ft/ s 2 = 32.1   s -1

Passo 5

  1. Período.

    2. τ n = 2 π ω n = 2 π 32.1 = 0.1957   s

    Passo 6

x 0 = x 0 m sin ⁡ ω n t + ϕ

Em t = 0,

x ˙ 0 = x 0 m ω n cos ⁡ ω n t + ϕ

t = 0

0 = x 0 m ω n cos ⁡ ϕ

Por isso

ϕ = π 2

t = 0

x 0 0 = 1 6   ft = x 0 m sin ⁡ ϕ = x 0 m 1

x 0 m = 1 6   ft

x ¨ 0 = - x 0 m ω n 2 sin ⁡ ω n t + ϕ

a 0 max = x ¨ 0 max = - x 0 m ω n 2 = - 1 6  ft 32.1   s -1 2 = 171.7   ft/ s 2

Resposta

a )   τ n = 0.1957   s

b )   a 0 max = 171.7   ft/ s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18.56. Determine a taxa de variação G da quantidade de movimento angular HG do disco do Problema 18.2.
18.49. Determine a energia cinética do paralelepípedo sólido do Problema 18.7
18.55. Determine a taxa de variação H D da quantidade de movimento angular HD do conjunto do Problema 18.1.
18.49. Determine a energia cinética do paralelepípedo sólido do Problema 18.7
18.58. Determine a taxa de variação G da quantidade de movimento angular HG do disco do Problema 18.4, admitindo que, no instante considerado, o conjunto tenha uma velocidade angular j e uma aceleraçã