Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 55

18.55. Determine a taxa de variação H D da quantidade de movimento angular HD do conjunto do Problema 18.1.

Passo 1

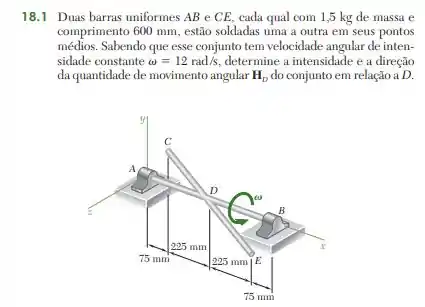
Vamos começar relembrando o problema 18.1. O problema fala de duas barras uniformes AB e CE que tem 15   k g de massa e 600   m m de comprimento cada, e estão soldadas uma a outra em seus pontos médios. A velocidade angular do sistema é ω = 12   i ^ r a d s .

O sistema é mais ou menos assim:

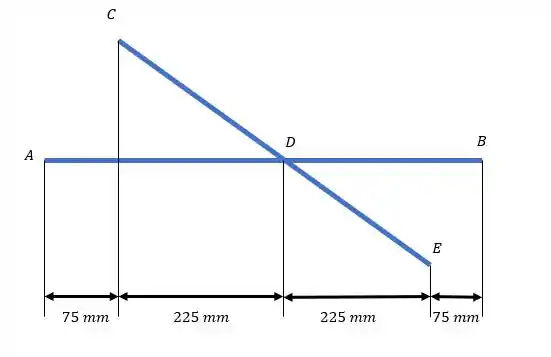
Passo 2

Vamos começar com a barra A B - :

I x ≈ 0

Olha só a barra está apontada na direção que está girando, e como a espessura da barra é desprezível podemos aproximar o momento de inércia para 0.

Então

H D = I x ⋅ ω   i ^ = 0

Agora vamos para a barra C E - . Para essa barra vamos usar os eixos principais x ' e y '

Para saber o valor de θ podemos usar o triângulo:

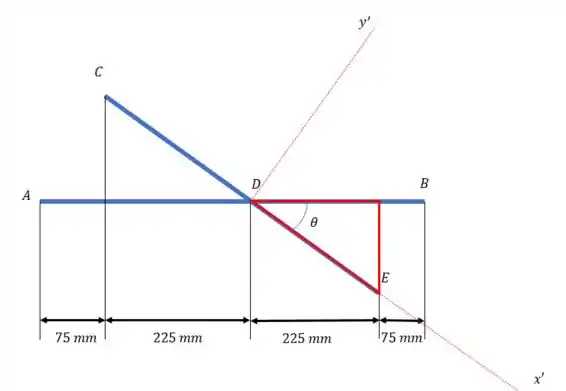
A gente sabe que D B = D E , então a hipotenusa do triângulo é 225 + 75 = 300   m m . Então podemos fazer

cos ⁡ θ = 225 300

θ = cos - 1 ⁡ 225 300 = 41,41 °

Agora vamos fazer

ω x ' = ω cos ⁡ θ = 12 ⋅ cos ⁡ 41,41 ° = 9 r a d s

E

ω y ' = ω ⋅ sin ⁡ θ = 12 ⋅ sin ⁡ 41,41 ° = 7,937 r a d s

Agora vamos calcular os momentos de inércia:

I x ' ≈ 0

E

I y ' = 1 12 m l 2 = 1 12 1,5 0 , 6 2 = 0,045

Beleza, agora temos tudo que precisamos para calcular a quantidade de momento angular H D .

H D = I x ' ω x '   i ^ ' + I y ' ω y '   j ^ '

Isso fica

H D = 0 + 0 , 045 7,937 = 0,357165   j ^ '

Agora tudo que resta fazer é converter H D para as coordenadas x e y .

H D = 0,357165 ⋅ ( sin ⁡ 41,41 °   i ^ + cos ⁡ 41,41 °   j ^ )

Isso fica

H D = 0,2362   i ^ + 0,2678   j ^

Passo 3

Beleza, agora vamos calcular a variação de H D , e para fazer isso basta que a gente calcule a derivada

H ˙ D = ω × H D

No nosso referencial rotativo ω = Ω .

H ˙ D = 12   i ^ × 0,2362   i ^ + 0,2678   j ^

Isso fica

H ˙ D = 0 + 3,21   k ^ = 3,21   N ⋅ m k ^  

E nós terminamos o problema aqui.

Resposta

H ˙ D = 3,21   N ⋅ m k ^  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento de um disco rotativo em banho de óleo é definido pela relação θ = θ 0 1 - e - t 4 , sendo θ expresso em radianos e t em segundos. Sabendo que θ =0,40r a d , determine a coordenada, a veloc
O conjunto mostrado na figura consiste uma haste reta A B C que passa através de uma placa retangular D E F H e está soldada. O conjunto gira em torno do eixo A C com uma velocidade angular constante
Uma série de pequenos componentes de máquina movidos por uma correia transportadora passa sobre uma polia esticadora de 150m m de raio. No instante mostrado na figura, a velocidade angular da polia es
A aceleração angular de uma placa circular de 600m m de raio mostrada na figura é definida pela relação α = α 0 e - t . Sabendo que a placa está em repouso quando t = 0 e que α 0 = 10r a d / s 2 , det
Uma série de pequenos componentes de máquina movidos por uma correia transportadora passa sobre uma polia esticadora de 150m m de raio. No instante mostrado na figura, a velocidade do ponto A é de 400