Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 168
Ao lançar a âncora em 100 pés de água, um pequeno barco a motor inverte sua hélice, o que dá um empuxo reverso P = 800 lb. Um total de 400 pés de corrente da âncora à proa foi liberado. A corrente pesa 1,63 lb/pés e a força para cima devido à flutuabilidade da água é de 0,21 lb/pés. Calcule o comprimento l da corrente em contato com o fundo.
Passo 1
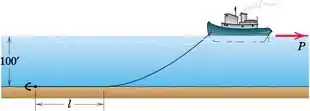
Primeiro, vamos desenhar o diagrama de corpo livre do barco, com a tensão da corrente TA, impulso P e a força de flutuabilidade FB atuando nele
Ao igualar a soma das forças na direção x a zero, podemos determinar a força T0
Podemos ver no esboço que as coordenadas do ponto A são
Também podemos ver que todo o comprimento da corrente é
Passo 2
Onde sA é o comprimento da parte OA da cadeia e s = 400. Sabendo disso, podemos escrever a expressão para o comprimento l como
Vamos escrever a expressão (19/05)
Observe que o peso total por metro é igual ao peso da corrente menos o efeito de flutuabilidade
Passo 3
Substitua e T0 por seus valores na expressão (5/19)
Em seguida, coloque as coordenadas do ponto A na equação
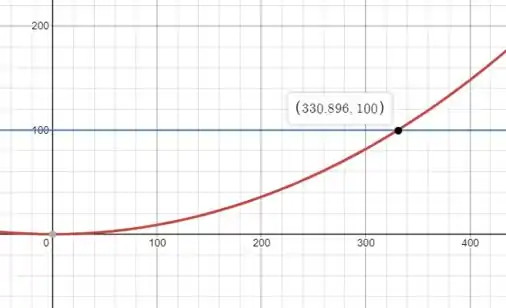
Usando uma calculadora gráfica como o Desmos (link nos comentários), representaremos as funções (y = 100) e e leremos os valores de xA que satisfazem ambas as equações do ponto de intersecção
Passo 4
A seguir, usando a expressão (5/20), determinaremos a parte O A da cadeia
Substitua T0, e xA por seus valores
Finalmente, vamos substituir sA por seu valor na expressão (1) para determinar o comprimento l