Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 165
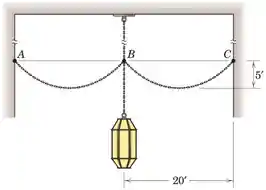
Uma luminária está suspensa no teto de um pórtico externo. Quatro correntes, duas das quais são mostradas, evitam o movimento excessivo do aparelho durante condições de vento. Se as correntes pesarem 15 libras por pé de comprimento, determine a tensão da corrente em C e o comprimento L da corrente BC.
Passo 1
Nesta tarefa, precisamos determinar a tensão em C e o comprimento da corrente BC. O peso das correntes é de 15 libras por pé.
diagrama de corpo livre
Primeiro, escreveremos a equação da curva parabólica da cadeia.
Passo 2
Agora vamos determinar a tensão no ponto C
E, finalmente, determinaremos o comprimento da corrente
Resposta
Exercícios de Livros Relacionados
Determine o centróide do sólido gerado pela revolução da parte da curva senoidal mostrada na figura em torno do eixo y . (Dica: use uma casa cilíndrica delgada de raio r e espessura d r como elemento
Os lados e a base de uma poncheira têm espessura uniforme t . Se t ≪ R e R = 250m m , determine a localização do centro de gravidade ( a ) da poncheira, ( b ) do ponche.
Determine o centroide da seção mostrada na figura, que foi obtida pelo corte de um cilindro elíptico por um plano inclinado.
Mostre que, para uma pirâmide regular de altura h e n lados n = 3 ,4 ,… , o centroide do volume da pirâmide está localizado a uma distância h / 4 acima da base.
Determine o centróide do sólido gerado pela revolução da parte da curva senoidal mostrada na figura em torno do eixo x .