Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 162
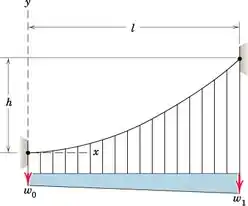
O cabo de luz tem inclinação zero em seu ponto inferior de fixação e suporta a carga unitária que varia linearmente com x de w0 a w1 conforme mostrado. Derive a expressão para a tensão no cabo na origem.
Passo 1
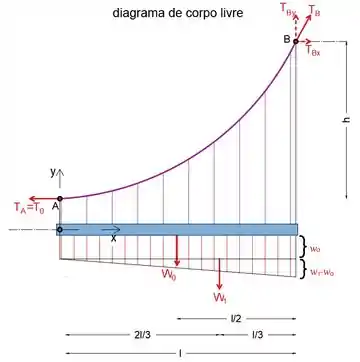
Primeiro, vamos desenhar o diagrama de corpo livre de todo o sistema
Observe que substituímos as cargas distribuídas por suas resultantes
Observe também que, uma vez que a inclinação no ponto A é igual a zero, a tensão TA é horizontal, ou seja,
Passo 2
Ao igualar a soma dos momentos sobre o ponto B a zero, podemos determinar a tensão T0
Substitua W0 e W1 por expressões escritas na Etapa 1.
A partir daqui, podemos expressar T0 como:
E a expressão final é:
Resposta
Exercícios de Livros Relacionados
Determine o centróide do volume obtido pela rotação da área sombreada da figura sobre o eixo x .
Determine o centroide da seção mostrada na figura, que foi obtida pelo corte de um tubo circular fino por dois planos inclinados.
Depois de nivelar um lote, um construtor coloca quatro estacas para indicar os cantos da base para uma casa. Para prover uma base nivelada firme, o construtor coloca um mínimo de 75 mm de brita abaixo
Determine o centróide do sólido obtido pela rotação da área sombreada da figura em torno da linha x = h .
Determine por integração direta os valores de x - para os dois sólidos obtidos passando-se um plano de corte vertical através da forma dada na Fig. 5.21. O plano de corte é paralelo à base da forma da