Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 88

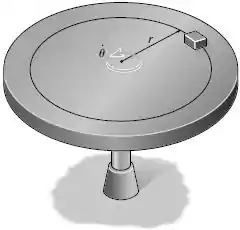
Se o coeficiente de atrito estático entre o bloco de massa m e a plataforma giratória é μ s , determine a velocidade angular constante máxima da plataforma que não faça com que o bloco escorregue.

Passo 1

O enunciado nos dá as seguintes informações:

Massa do bloco: m

Coeficiente de atrito estático: μ s

Como o bloco está sobre uma plataforma, teremos a ação da força normal N .

Devido ao movimento giratório desta plataforma e ao coeficiente de atrito entre ela e o bloco, sabemos que também existirá uma força de atrito F resultante. Sabemos que a fórmula para a força de atrito é dada por

F = μ s N

Por estarmos usando coordenadas polares, esta força F terá componentes em r e em θ .

Desenhamos o diagrama de corpo de livre do bloco:

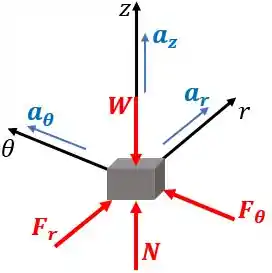
Onde W = m g é a força peso.

A partir desses dados, devemos determinar a velocidade angular θ ˙ constante máxima da plataforma que não faça com que o bloco escorregue.

Como não queremos que o bloco escorregue, r e z devem ser constantes durante o movimento, ou seja, seus valores não podem mudar pois isso significaria que o bloco se moveu em relação a plataforma. Além disso, sua velocidade angular deve ser igual a da plataforma pois ele estão se movendo juntos, como se o bloco estivesse colado nela.

Passo 2

Primeiramente, vamos encontrar as derivadas temporais do bloco em r ( r ˙ e r ¨ ). Como r é constante, seu valor não varia no tempo, resultando em

r ˙ = d r d t = 0   m / s

r ¨ = d 2 r d t 2 = 0   m / s 2

Agora analisaremos as derivadas temporais em θ ( θ ˙ e θ ¨ ). O valor de θ ˙ é o que queremos descobrir, porém sabemos que seu valor é constante. Logo,

θ ¨ = d θ ˙ d t = 0   r a d / s 2

Em seguida, vamos encontrar as derivadas temporais em z ( z ˙ e z ¨ ). Como z é constante, seu valor não varia no tempo, resultando em

z ˙ = d z d t = 0   m / s

z ¨ = d 2 z d t 2 = 0   m / s 2

Passo 3

Sabemos que as componentes da aceleração do bloco nas coordenadas r , θ e z são dadas por

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

a z = z ¨

Logo,

a r = r ¨ - r θ ˙ 2 = 0 - r θ ˙ 2 = - r θ ˙ 2   m / s 2

a θ = r θ ¨ + 2 r ˙ θ ˙ = r 0 + 2 0 θ ˙ = 0   m / s 2

a z = z ¨ = 0   m / s 2

Passo 4

Agora aplicaremos as Equações do Movimento.

Analisando primeiramente no eixo r , temos que

∑ F r = m a r

F r = m - r θ ˙ 2 = - m r θ ˙ 2  

Analisando no eixo θ , temos

∑ F θ = m a θ

F θ = m ( 0 ) = 0

Analisando no eixo z , temos

∑ F z = m a z

N - W = m ( 0 )

N = W = m g

Sabemos que a força F resultante no bloco é dada por

F = F r 2 + F θ 2 + F z 2

Logo,

F = - m r θ ˙ 2 2   + 0 2 + 0 2 = m r θ ˙ 2  

Passo 5

Unindo as informações, temos que

F = m r θ ˙ 2 = μ s N

Substituindo o valor de N , ficamos com

m r θ ˙ 2 = μ s m g

Logo,

θ ˙ 2 = μ s g r

θ ˙ = μ s g r

Esta é a velocidade angular do bloco. Como sabemos que o bloco tem a mesma velocidade angular da plataforma, esta será a resposta do problema.

Resposta

θ ˙ = μ s g r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Antes das missões Apollo para a Lua, várias espaçonaves “Lunar Orbiter” foram utilizadas para fotografar a superfície lunar a fim de obter informações a respeito de possíveis locais para pouso. Na con
Deduza a terceira lei do movimento planetário de Kepler das Eqs. (12.39) e (12.45).
Ao aproximar-se do planeta Júpiter, uma nave espacial libera uma sonda que entra na atmosfera do planeta no ponto B a uma altitude de 450 km acima da superfície do planeta. A trajetória da sonda é uma
Um ônibus espacial está descrevendo uma órbita circular a uma altitude de 350 mi acima da superfície da Terra. Quando passa pelo ponto A, ele aciona seu motor por um curto intervalo de tempo para redu
a) Expresse a excentricidade da órbita elíptica descrita por um satélite em torno de um planeta em termos das distâncias r0 e r1 correspondentes, respectivamente, ao perigeu e ao apogeu da órbita. (b)