Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 115

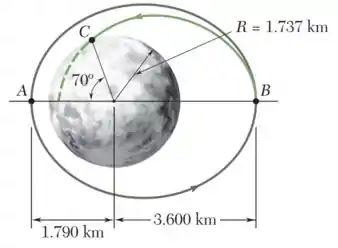
Antes das missões Apollo para a Lua, várias espaçonaves “Lunar Orbiter” foram utilizadas para fotografar a superfície lunar a fim de obter informações a respeito de possíveis locais para pouso. Na conclusão de cada missão, a trajetória da espaçonave era ajustada de modo que a espaçonave colidisse com a Lua para estudar ainda mais as características da superfície lunar. A órbita elíptica do “Lunar Orbiter 2” é mostrada na figura. Sabendo que a massa da Lua é 0,01230 vezes a massa da Terra, determine em quanto a velocidade escalar dessa espaçonave deve ser reduzida no ponto B de modo que ela colida na superfície lunar no ponto C. (Dica: O ponto B é o apogeu da trajetória elíptica de impacto.)

Passo 1

Vamos lá pra mais uma questão, partiu? O enunciado pede que a gente determine em quanto a velocidade escalar dessa espaçonave deve ser reduzida no ponto B de modo que ela colida na superfície lunar no ponto C.

Da solução do Problema 12.102, nós temos a órbita eliptica AB

1 r A + 1 r B = 2 G M l u a h A B 2

Onde

h A B = ( h B ) A B = r B ( v B ) A B

e

G M l u a = G ( 0.01230 M t e r r a )   = 0.01230 g R ² t e r r a           u s a n d o   E q .   ( 12.30 )

Então

1 r A + 1 r B = 2 ( 0.01230 g R 2 t e r r a ) [ r B v B A B ] ²

ou

v B A B = R 2 t e r r a r B 0.0246 g 1 r A + 1 r B 1 / 2 = 6.37 × 10 6 m 3600 × 10 3 m 0.0246 × 9.81 m / s 2 1 1790 × 10 3 m + 1 3600 10 3 m 1 / 2

= 950.43   m / s

Passo 2

Para a tragetória de impacto eliptica, nós temos

1 r = G M l u a h B C 2 + C   c o s ∅               [ E q . 12.39 ]

Onde

h B C = ( h B ) B C = r B ( v B ) B C

Notando que o Ponto B é o apogeu da tagetória, nós temos

a B, ∅ = 180 o : 1 r B = G M l u a h B C 2 - C

C = G M l u a h B C 2 - 1 r B

a C, ∅ = - 70 o : 1 R = G M l u a h B C 2 + C   c o s ⁡ ( - 70 o )

C = 1 c o s ⁡ 70 o 1 R - G M l u a h B C 2

Então G M l u a h B C 2 - 1 r B = 1 c o s ⁡ 70 o 1 R - G M l u a h B C 2

h B C 2 = G M l u a ( 1 + cos ⁡ 70 o ) 1 R + c o s ⁡ 70 o r B

( v B ) B C = R t e r r a r B 0.012309 ( 1 + cos ⁡ 70 o ) 1 R + c o s ⁡ 70 o r B 1 / 2

( v B ) B C = 6.37 × 10 6 m 3600 10 3 m 0.01230 ( 9.81 m s 2 ) ( 1 + cos ⁡ 70 o ) 1 1737 × 10 ³ m + c o s ⁡ 70 o 3600 × 10 3 m 1 / 2 = 869.43   m / s

Passo 3

Finalmente, ( v B ) B C = ( v B ) A B + ∆ v B

ou, ∆ v B = 869.43 - 950.43 m / s

ou

∆ v B = 81.0   m / s

Resposta

∆ v B = 81.0   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo do repouso, uma lancha desloca-se ao longo da trajetória circular ρ = 50m , a uma velocidade escalar v = 0,8tm / s , onde t é dado em segundos. Determine as intensidades da velocidade e acele
O carro passa o ponto A com uma velocidade escalar de 25m / s , após o qual a sua velocidade escalar é definida por v = 25 - 0,15 sm / s . Determine a intensidade da aceleração do carro quando ele che
Um trem passa pelo ponto B com uma velocidade escalar de 20m / s , a qual está diminuindo em a t = - 0,5m / s 2 . Determine a intensidade da aceleração do trem neste ponto.
Um automóvel tem velocidade escalar de 24m / s no ponto A e tem aceleração a , tendo intensidade de 3m / s 2 , atuando na direção mostrada. Determine o raio de curvatura da trajetória no ponto A e a c
O trem passa o ponto A com uma velocidade escalar de 30m / s e começa a reduzir sua velocidade escalar a uma razão constante de a t = - 0,25m / s 2 . Determine a intensidade da aceleração do trem quan