Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 40

O coeficiente de atrito estático entre o tambor e a barra de freio é μ s = 0,4 . Se M = 35   N ⋅ m determine a menor força P que precisa ser aplicada à barra de freio a fim de impedir que o tambor gire. Além disso, determine as componentes horizontal e vertical correspondentes da reação no pino O . Despreze o peso e a espessura da barra de freio. O tambor tem uma massa de 25   k g .

Passo 1

O problema pede que encontremos a menor força P que precisa ser aplicada à barra de freio e as componentes horizontal e vertical correspondentes da reação no pino O .

Vamos começar usando as equações de equilíbrio para o momento, aquelas lá:

∑ M O = 0

∑ M A = 0

Primeiro no eixo O :

35 - F B ( 0,125 ) = 0

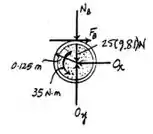
Assim, descobrimos a reação em B :

F B = 280   N

Agora, o momento no eixo A :

P 1 + 280 0,5 - N B ( 0,7 ) = 0

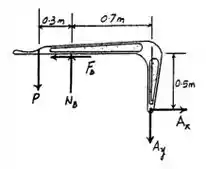
Passo 2

Agora, amos aplicar os coeficientes de atrito estático, lembra que eles agem em relação á normal.

Então fica:

F B = 280 = μ s N B = 0,4 N B

Então, encontramos a normal em B :

N B = 700   N

Agora, substituímos N B no momento em A , assim:

P 1 + 280 0,5 - ( 700 ) ( 0,7 ) = 0

Assim, temos que:

P = 350   N

Passo 3

Por fim, vamos pegar a equação de equilíbrio para as forças:

∑ F y = 0

O y - 245,25 - 700 = 0

Então, achamos:

O y = 945   N

E no eixo x agora:

∑ F x = 0

280 - O x = 0

O x = 280   N

Resposta

N B = 700   N

P = 350   N

O y = 945   N

O x = 280   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a corda der três voltas completas mais a volta básica ( 165 ° ) em torno do pino, determine se o homem de 80k g pode evitar que a caixa de 300k g se mova. Os coeficientes de atrito estático entre a
A viga uniforme de 25k g está apoiada pela corda que está à ponta da viga, passa pelo pino rugoso e depois é conectada ao bloco de 50k g . Se o coeficiente de atrito estático entre a viga e o bloco e
Um cilindro D de 10k g , que está preso a uma pequena polia B , é colocado na corda conforme a figura. Determine o maior ângulo θ de modo que a corda não deslize pelo pino em C . O cilindro em E tem u
Se uma força P = 200N é aplicada ao cabo da alavanca em L , determine o torque máximo M que pode ser resistido de modo que o volante não esteja na iminência de girar no sentido horário. O coeficiente
Um fazendeiro de 90k g tenta evitar a vaca escape enrolando a corda com duas voltas em torno do tronco da árvore, como mostra a figura. Se a vaca exerce uma forca de 125N sobre a corda, determine se o