Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 12

Os coeficientes de atrito são e entre todas as superfícies de contato. Determine a menor força necessária para iniciar o movimento do bloco de 30 kg se o cabo AB está ligado tal como mostra a figura, é removido.

Passo 1

Tá legal! Vamos começar o exercício desenhando o DCL do bloco de cima:

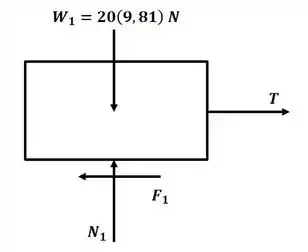
Vamos aplicar o somatório de forças na direção para descobrir o valor da reação normal:

Agora podemos calcular o valor da força de atrito :

Agora aplicando o somatório de forças na direção para encontrar o valor de :

Passo 2

Agora vamos desenhar o DCL para o bloco de baixo:

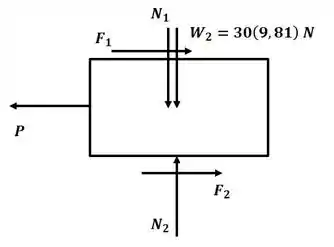
Agora vamos aplicar o somatório de forças na direção :

Agora podemos calcular o valor da força de atrito :

Agora aplicando o somatório de forças na direção para encontrar o valor de :

Passo 3

Agora vamos desenhar o DCL do sistema para o caso em que não temos a corda AB:

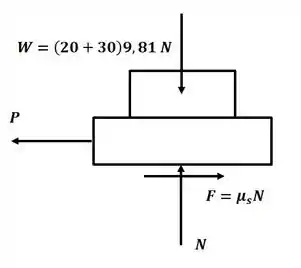
Agora vamos aplicar o somatório de forças na direção :

Agora podemos calcular o valor da força de atrito :

Agora aplicando o somatório de forças na direção :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/38) Se o coeficiente de atrito entre o cilindro semicircular sólido e o plano inclinado é 0,30 , determine o valor máximo do ângulo θ com a horizontal até o qual o plano pode ser inclinado antes que

6/45) A barra esbelta uniforme é abaixada lentamente desde sua posição ereta ( θ = 90 ° ) por meio do cabo preso a sua extremidade superior e que passa sob a pequena polia fixa . Se a barra escorrega

6/42) A viga em I uniforme , de massa m é apoiada em suas extremidades sobre dois trilhos horizontais fixos como mostrado . Determine a força horizontal máxima P que pode ser aplicada sem fazer com qu

6/49) O freio de bloco duplo mostrado é aplicado ao rotor por meio da ação da mola. Para soltar o freio , uma força P é aplicada na barra de controle . Na posição de operação com P = 0 , a mola está c

6/48) Um bloco de massa m 0 é colocado entre a parede vertical e o pequeno rolete ideal na extremidade superior , A , da barra esbelta uniforme de massa m . A extremidade inferior , B , da barra repou