Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 38
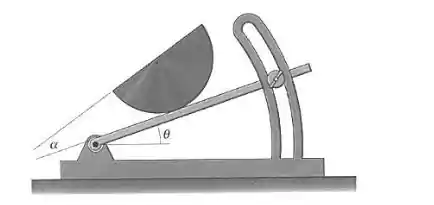
6/38) Se o coeficiente de atrito entre o cilindro semicircular sólido e o plano inclinado é , determine o valor máximo do ângulo com a horizontal até o qual o plano pode ser inclinado antes que o cilindro escorregue . Para essa condição , qual é o ângulo correspondente pelo qual o cilindro terá girado em relação ao plano inclinado ?
Passo 1
Então galera , a primeira coisa que devemos fazer é analisar o triângulo indicado pela figura do enunciado .
Para acharmos o terceiro ângulo desconhecido , devemos lembrar que a soma dos ângulos internos de um triângulo é igual a () , sendo assim :
Dessa forma , pela lei dos senos :
Logo ,
Passo 2
Bom pessoal , como exposto neste capítulo do livro e demonstrado em exercícicios anteriores , o valor máximo do ângulo formado pela força de atrito ocorre quando :
Consequentemente , utilizando a relação :
Achamos que
Dessa forma .
Logo ,
Resposta
Tranquilo pessoal? Então partiu resolver mais questões