Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 61
Um colar de 500 g pode deslizar sem atrito sobre uma barra curva BC em um plano horizontal. Sabendo que o comprimento indeformado da mola é de 80 mm e que k = 400 kN/m, determine (a) a velocidade que o colar deve receber em A para atingir B com velocidade nula, (b) a velocidade do colar quando ele finalmente atingir C.
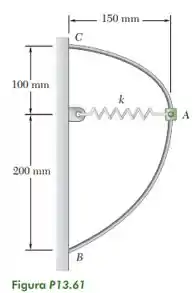
Fonte: Beer – Dinâmica – 9ª ed
Passo 1
Olá meus amores, tudo bem?
Espero que sim! Vamos para mais uma atividade dessa disciplina maravilhosa!!
Bem, como de costume nas questões de trabalho e/ou energia, podemos analisar o problema pelo diagrama do corpo livre ou por conservação de energia.
Aqui, utilizemos a conservação de energia. Ou seja, durante todo o deslizamento do colar pela barra BC, podemos utilizar as parcelas de energia cinética, potencial e potencial elástica:
Assim, admitimos que:
Entretanto, vamos ler novamente o início do enunciado do nosso problema: “Um colar de 500 g pode deslizar sem atrito sobre uma barra curva BC em um plano horizontal”. Podemos então, desconsiderar a ação da força gravitacional em toda a curva. Assim, obtemos a expressão para nosso problema:
Passo 2
Letra a) Pronto, já temos nossa expressão principal. Agora vamos reescrevê-la de forma mais esmiuçada:
Ok, como o enunciado diz que , então:
Tudo beleza até aqui pessoal? Até agora nós aplicamos conservação de energia no problema e consideramos o que o enunciado nos falou.
Agora, lembremos que as deformações são calculadas pela distância para os pontos menos o comprimento natural da mola, que foi indicado no enunciado de . Portando, temos:
Isolando o , obtemos:
Passo 3
Letra b) Para descobrir a velocidade em C, podemos utilizar na mesma fórmula da conservação da energia. Fica a critério “comparar” o ponto C com A ou B. Vamos analisar o ponto C em relação ao B (fica menos trabalhoso, pois já sabemos que a ).
E, seguindo o mesmo critério, temos:
E novamente, isolando :
Resposta
Portanto:
Letra a)
Letra b)