Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 31
Um bloco de 3 kg está preso a um cabo e uma mola como mostrado na figura. A constante de mola é e a tração no cabo é 15 N. Se o cabo é cortado, determine (a) o máximo deslocamento do bloco, (b) a máxima velocidade do bloco.
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão!
Mas, não é por isto que não devemos identificar as forças do nosso problema e construir um diagrama de corpo livre. Portanto, este é o nosso primeiro passo (e até o mais importante!).
Então, fazendo o diagrama de corpo livre, temos,
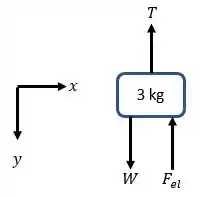
OBS: iremos assumir a origem do sistema de coordenadas no ponto em que a corda é rompida.
Passo 2
Agora é importante identificarmos quem é cada uma das nossas forças e qual é a deformação inicial (caso exista) da nossa mola!
Em relação as forças, para o nosso bloco temos a presença da força peso, , a força de tração na corda e a força elástica . Como inicialmente o bloco está em equilíbrio estático, temos:
Pelo sinal da força, sabemos na verdade que a mola está comprimida. Para os próximos passos, é importante termos bastante cuidado com a unidade da constante Ela é ou
Passo 3
Agora, podemos partir para o cálculo dos termos de trabalho e energia cinética. Quando temos (ponto em que é cortado a corda), a velocidade do bloco é . Já para um ponto qualquer, teremos . Assim, temos os seguintes termos de energia cinética:
Em relação aos trabalhos das forças, começando pela força peso, temos:
Já para o trabalho da força elástica, ele será:
Logo,
Passo 4
Agora, para resolvermos a letra a), basta aplicarmos o princípio de trabalho e energia e avaliar o valor de quando (máxima deformação ocorre quando a velocidade é nula – mudará de sentido).
Desta forma,
Assim, chegamos ao valor de , o qual ocorre para baixo!
Passo 5
Já para a letra b), precisamos determinar a velocidade máxima do bloco. Esta velocidade será atingida quando o trabalho das forças for igual a zero (a aceleração no bloco será nula). Lá das disciplinas de cálculo aprendemos que isto irá ocorrer no ponto tal que:
Como queremos a velocidade máxima, pelo princípio do trabalho e energia, temos:
E assim finalizamos a questão!