Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 101
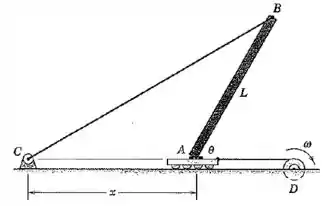
A figura mostra a vista lateral de uma laje de concreto uniforme com uma massa de . A laje está sendo içada lentamente pelo guincho por meio do cabo preso ao carrinho. Na posição , a distância desde a posição fixa no solo até o carrinho é igual ao comprimento da laje . Se o cabo de elevação se rompe nesta posição, determine a aceleração inicial do carrinho, cuja masssa é desprezível, e a tração inicial no cabo fixo. A extremidade da laje não desliza sobre o carrinho
Passo 1
Vamos começar olhando para as forças que agem sobre a laje no caso em que .
Podemos montar algumas equações a partir desse desenho. Começando pelo mais simples: a segunda lei de Newton na direção horizontal:
Escolhemos essa direção porque estamos interessados na força , e não conhecemos a força , que é completamente vertical:
E vamos chamar de a componente da aceleração do centro de massa da laje na direção , então:
A partir do mesmo desenho, também podemos montar uma equação de momentos em relação ao ponto , de forma que a força desconhecida tenha momento nulo:
E o momento de inércia da laje em relação a um eixo que passa pelo ponto é:
Então:
Com isso ficamos com um sistema de duas equações:
Nós temos três variáveis desconhecidas (, e ), mas apenas duas equações. Podemos encontrar de outro jeito para resolver esse problema.
Passo 2
Vamos fazer um diagrama (fora de escala) com as acelerações de cada extremidade e do centro de massa no instante em que o cabo se rompe:
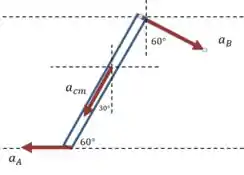
Vamos continuar usando o ponto como referência, e escrever as acelerações de e do em relação a esse ponto:
E é fácil escrever as acelerações relativas e , quando consideramos que a barra tem uma aceleração angular em torno do ponto (a mesma que usamos na nossa equações de momentos lá no primeiro passo):
Além disso essas duas acelerações relativas terão a mesma direção. Podemos representar tudo isso em um único diagrama (aproveite o desenho anterior para entender de onde vieram os ângulos representados aqui):
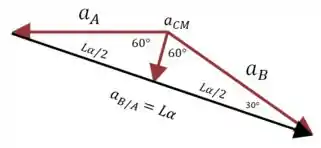
Podemos usar esse diagrama para encontrar :
E a componente de na direção , que é a direção de é:
Passo 3
Vamos substituir essa informação no sistema que escrevemos lá em cima:
E agora podemos resolver esse sistema (de duas equações e duas variáveis) para encontrar :
Substituindo a segunda equação na primeira, encontramos o seguinte:
Passo 4
E agora falta apenas calcular a acelerção do carrinho. Vamos voltar ao nosso diagrama de acelerações:
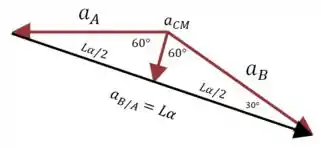
Daqui fica fácil ver que:
E podemos encontrar usando o nosso sistema de equações do passo anterior, e o resultado que acabamos de obter para :
Então:
Resposta
A tração inicial é , e a aceleração do carrinho é .