Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 156

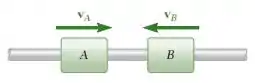
Os colares A e B , de mesma massa m , movem-se um em direção ao outro com as velocidades mostradas na figura. Sabendo que o coeficiente de restituição entre os colares é 0 (impacto plástico), mostre que após o impacto ( a ) a velocidade comum dos colares é igual à metade diferença entre suas velocidades antes do impacto, ( b ) a perda de energia cinética é 1 4 m v A +   v B 2 .

Passo 1

Fala aí, galera. Beleza? Bora fazer mais um exercício. Primeiro, sabemos que em um impacto plástico, dois corpos de mesma massa permanecem juntos após o impacto, com a mesma velocidade e no mesmo sentido, ou seja:

m v A - m v B = 2 m v '

Isolando v ' , temos que a velocidade dos colares vai ser:

v ' = 1 2 ( v A - v B )

Opa, conseguimos provar o que o problema nos pediu na letra ( a ) . Bora pra letra ( b ) .

Passo 2

Em seguida, precisamos provar que a perda de energia cinética desse sistema é 1 4 m v A +   v B 2 . Para isso, vamos determinar a energia cinética antes e depois do sistema, assim, podemos encontrar a energia perdida. Portanto, teremos a seguinte relação:

E n e r g i a   p e r d i d a = T 1 - T 2

Onde T 1 é a energia cinética antes do impacto e T 2 a energia cinética depois do impacto. Temos:

E n e r g i a   p e r d i d a = T A + T B - T A ' + T ' B E n e r g i a   p e r d i d a = 1 2 m v A 2 + v B 2 - 1 2 m 1 2 2 v ' 2

Vamos utilizar a velocidade após o impacto que encontramos na primeira parte do problema. Substituindo:

E n e r g i a   p e r d i d a = 1 2 m v A 2 + v B 2 - 1 2 m 1 2 2 1 2 v A - v B 2

Resolvendo esta equação, temos que a energia perdida vai ser dada por:

E p = 1 4 m v A + v B 2

Como podemos ver, é a mesma relação que o enunciado nos deu.

Isso é tudo, pessoal! Bora fazer mais questões para ficar craque.

Resposta

v ' = 1 2 ( v A - v B )

E p = 1 4 m v A + v B 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pequena bola balança em um círculo horizontal na extremidade de uma corda de comprimento ∫ 1 , que forma um ângulo θ 1 com a vertical. A corda é então puxada lentamente pelo suporteem O até que o
Duas discotecas de hóquei idênticos movem-se sobre uma pista de hóquei a uma mesma velocidade de 3 m / s em sentidos paralelos e opostos quando se chocam do modo que é visto na figura. Admitindo um co
Um dos requisitos para as bolas de tênis usadas em competições oficiais é que, quando caem em uma superfície rígida de uma altura de 2,5 m, a altura do primeiro rebote da bola deve estar na faixa de 1
Duas bolas de bilhar idênticas de 47,4m m de diâmetro podem mover-se para aparecer em uma mesa de bilhar. A bola B está em repouso e a bola A tem uma velocidade inicial v = v 0 i . (a) Sabendo que b =
Uma bola A de 600g move-se com velocidade de 6m / s de intensidade quando é atingida por uma bola B de 1k g que tem velocidade de 4m / s de intensidade. Sabendo que o coeficiente de restituição é 0,8