Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 93

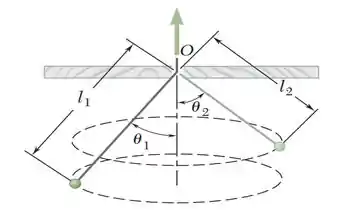
Uma pequena bola balança em um círculo horizontal na extremidade de uma corda de comprimento ∫ 1 , que forma um ângulo θ 1 com a vertical. A corda é então puxada lentamente pelo suporteem O até que o comprimento da ponta livre seja de ∫ 2 .

(a) Deduza uma relação entre, ∫ 1 , ∫ 2 , θ 1   e θ 2 .

(b) Se a bola é posta em movimento de modo que inicialmente ∫ 1 = 0,8 m e θ 1 = 35°, determine o ângulo θ 1 quando θ 2 = 0,6m.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente deduza relações de comprimento e se a bola passar em diferentes posições :D

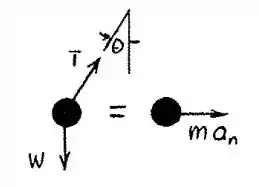
  1. Para o estado 1 ou 2 negligenciando o componente vertical da aceleração,

+ ↑ ∑ F y = 0 : T   c o s   θ - W = 0

T = W   c o s  

+ → ∑ F x = m a n   :   T   s i n   θ   c o s   θ = m v ² ρ

Mas ρ = l   s i n   θ   de modo a

v 2 = l W m   s i n 2 θ   c o s   θ =   l   g   s i n   θ   t a n   θ

v 1 =   l 1     g   s i n   θ 1   t a n   θ 1

v 2 =   l 2     g   s i n   θ 2   t a n   θ 2

E ∑ M y = 0 : H y = c o s t a n t e

r 1 m v 1 =   r 2 m v 2 ou v 1 l 1   s i n   θ 1 = v 2 l 2   s i n   θ 2

l 1 3 / 2   g   sin ⁡ θ 1 s i n   θ 1   t a n θ 1 =   l 2 3 / 2 sin ⁡ θ 2 s i n   θ 2   t a n θ 2

l 1 3   sin ⁡ ³ θ 1   t a n   θ 1 = l 2 3   sin ⁡ ³ θ 2   t a n   θ 2

Passo 2

(b)Com θ 1 =35°, l 1 = 0.8   m ,   e l 2 = 0.6   m ,  

0.8 3 s i n 3 35 °   t a n   35 ° = 0.6 3 s i n   ³   θ 2 t a n   θ 2

s i n θ 2 3 t a n   θ 2 - 0 = 43.6 °

Resposta

a) l 1 3   sin ⁡ ³ θ 1   t a n   θ 1 = l 2 3   sin ⁡ ³ θ 2   t a n   θ 2

b) θ 2 = 43.6 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva as equações diferenciais definindo (a) os deslocamentos da massa me do Ponto A, (b) as cargas nos capacitores do análogo elétrico.
O cano da arma de caça tem massa de 750 g e é retornado para a posição de tiro após o recuo de um recuperador de constante c = 18 kN s/m. Determine (a) a constante k que deveria ser usada para o recup
Um vagão de trem carregado de massa 15.000 kg está circulando a uma velocidade constante v 0 , quando é acoplado com uma mola e um sistema amortecedor (Fig. 1). O registro da curva deslocamento--tempo
Considere o circuito do Problema 19.153 quando o capacitor C é removido. Se a chave S for fechada no tempo t = 0 determine (a) o valor final da corrente no circuito, (b) o tempo t no qual a corrente t
Um elemento de máquina de 200 lb apoiado por quatro molas, cada uma com k = 12 lb / ft constante, é submetido a uma força periódica de frequência 0,8 Hz e amplitude de 20 lb. Determine a amplitude da