- Coloque seu lápis sobre a posição da sua melhor estimativa visual do centroide da área triangular. Verifique a posição horizontal da sua estimativa referindo-se aos resultados do Exemplo 5/2.
Passo 1
Se redesenharmos a figura da questão como dois triângulos retângulos formados entre os pontos ABD e ACD:
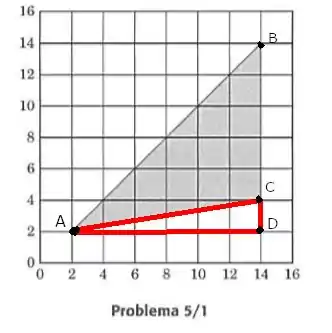
Passo 2
O centro de massa do triângulo ABD é:
E sua área será de:
Onde é tomada de acordo com a origem do sistema e a medida da área é a diferença entre seu ponto inicial e o final no caso .
Passo 3
Para o triângulo teremos:
Já a área:
Uma vez que esse triângulo não existe e queremos retirar sua área para poder encontrar o seu centro de massa.
Passo 4
Aplicando a seguinte fórmula para encontrar
O que dá:
Porém na escala de 8 a 10, está mais para 10 do que 8. Logo aponte o lápis para o 10, uma vez que não para dizer onde é o 9.333.