Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 82

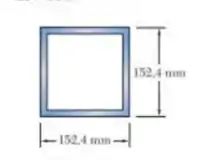
Um tubo estrutural quadrado com a seção transversal mostrada é usado como uma coluna de 6096   m m de comprimento de flambagem para suportar uma força centrada de 289   k N . Sabendo que os tubos disponíveis para uso são feitos com espessuras de parede variando entre 6,35   m m e 19,05   m m com incrementos de 1,587   m m , utilize o método da tensão admissível para determinar o tubo mais leve que pode ser usado. Use σ E =   248,2   M P a e E   =   200 G P a .

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine o tubo mais leve que pode ser usado temos os seguintes dados:

b o = 6   i n . b i = b o - 2 t A = b o 2 - b i 2

I = 1 12 ( b o 4 - b i 4 )

L e = 20   f t = 240   i n P = 65   k i p s

σ Y = 36   k s i E = 29   ×   10 6   p s i = 29 ×   10 3   k s i

Passo 2

Aço:Transição L e / r : 4,71 E σ Y = 4,71 29,000 36 = 133,68

Tentar t = 1 2   i n . = 0,5   i n b i = 5,0   i n . A = 6 2 - 5,0 2 = 11   i n 2

I = 1 12 [ ( 6 ) 4 - ( 5,0 ) 4 ] = 55,9167   i n 4

r = I A = 2,2546   i n

L e r = 240 2,2546 = 106,449 > 133,68

σ e = π 2   E ( L e / r ) 2 = π 2 ( 29   ×   10 3 ) ( 106,442 ) 2 = 25,262   k s i

σ c r = ( 0,658 σ y / σ e ) σ y = [ 0,658 36 / 25,262 ] ( 36 ) = 19,827

P a l l = σ c r A 1,67 = ( 19,827 ) ( 11 ) 1,67 = 130,60   k i p s

Passo 3

P a l l é aproximadamente proporcional a t

t 0,5 ≈ 65 130,6 t ≈ 0,249   i n

Tentar t = 1 4   i n = 0,25   i n b i = 5,5   i n A = 5,75   i n 2

I = 1 12 [ ( 6 ) 4 - ( 5,5 ) 4 ] = 31,745   i n 4 r = I A = 2,3496   i n

L e r = 240 2,3496 = 102,143 > 133,68

σ e = π 2 ( 29   ×   10 3 ) ( 102,143 ) 2 = 27,433   k s i

Passo 4

σ c r = [ 0,658 36 / 27,433 ] ( 36 ) = 20,786   k s i

P a l l = σ c r A 1,67 = ( 20,786 ) ( 5,75 ) 1,67 = 71,5   k i p s > 65   k i p s

= 1 / 4   i n .

Resposta

1 / 4   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2. A coluna é composta por um elemento estrutural rígido preso por um pino na base e acoplado a uma mola no topo. Se a mola não estiver esticada quando a coluna estiver em posição vertical, determine
1. Determine a carga de flambagem crítica para a coluna. Podemos considerar que o material é rígido.
5. Uma barra quadrada é feita de plástico PVC com módulo de elasticidade E = 9 G P a e deformação por escoamento ∈ e = 0,001m m / m m . Determine as dimensões a de sua menor seção transversal, de modo
6. A haste é feita de açoA - 36 . Determine, com aproximação de 1m m , o menor diâmetro da haste que suportará a carga P = 25k N sem flambagem. As extremidades estão apoiadas em roletes.
A haste é feita de aço com 25 mm de diâmetro. Determine a carga crítica de flambagem, se as extremidades estiverem apoiadas em roletes.E a ç o = 200G P a ç , σ e = 350M P a .