Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 42a
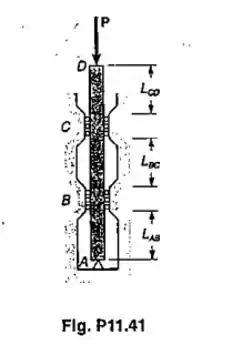
Para a coluna do Prob.11.41, sabendo-se que L_AB=0,9m, determinar:(a) os maiores comprimentos LBC e LCD que podem ser usados, se a carga admissível P deve ser tanto maior quanto possível;(b) a intensidade da correspondente carga admssível.
Passo 1
Fala pessoal, vem comigo pra mais essa?
Vamos trazer alguns valores do exercício 41, pois o nosso problema é baseado nele tá?
Esse exercício traz pra gente o conceito de coeficiente de flambagem e ele vai entrar no comprimento efetivo do peso crítico:
E o peso crítico alterado fica:
Bom o nosso problema é um pouco diferente dos que temos visto, essa coluna tem vários travamentos e a chave pra resolver a questão é justamente os tipos de travamento. Foi dito que os roletes travam a rotação então funcionam como engaste, já o pino em A permite o giro, vamos desenhar as deformações e definir para cada trecho um coeficiente de flambagem.
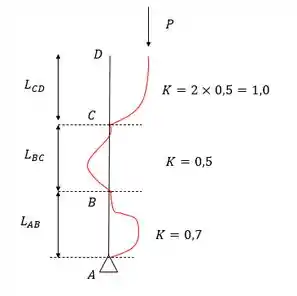
O problema nos dá o valor do trecho e pede o maior valor dos outros dois trechos de forma que seja máximo, então vamos fazer o seguinte: calcular o peso crítico para o trecho que temos os valores e definir que teremos o mesmo peso crítico para o resto da coluna.
A gente vai fazer isso pois, não adianta um trecho da coluna resistir á um peso crítico mais alto, ela vai falhar para o menor deles. Da fórmula do peso crítico a gente vai isolar cada comprimento.
Passo 2
Vamos calcular o peso crítico para o trecho AB usando a fórmula:
mas antes precisamos do momento de inércia que é constante por toda a coluna.
E o comprimento do trecho é:
E o coeficiente de flambagem:
Daí:
Beleza vamos seguir com o nosso plano!
Passo 3
Como prometido vamos igualar o peso crítico e aqui começaremos pelo trecho BC:
E precisamos aqui lembrar que para o trecho BC:
E substituindo:
Isolando L, temos:
Daí:
E para o trecho CD, temos:
E lembrando que pela figura da deformação da coluna, temos o coeficiente do trecho CD:
Então igualamos:
E isolando o comprimento:
Daí: