Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 112

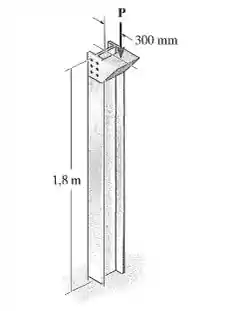
A coluna W310 33 de aço estrutural A-36 está engastada na base e é livre no topo. Se for submetida a uma carga P = 20 kN, determine se ela é segura com base nas equações AISC da Seção 13.6 e na Equação 13.30.

Passo 1

Fala aí galera, borá fazer mais um problema de resmat.

Como está engastada e livre

Calculando o índice de esbeltez limite:

Primeiramente, devemos determinar o menor raio de giração possível, que será o correspondente ao menor momento de inércia. Logo:

Com isso, podemos determinar o índice de esbeltez, que será:

Como é maior que o limite, teremos:

Passo 2

Agora, precisamos calcular alguns parâmetros:

Sabemos que nossa tensão máxima é dada por:

Sabemos que o momento é a força vezes a excentricidade.

Se substituirmos os dados na equação acima, teremos:

Como a tensão achada ultrapassou a admissível, não está adequado.

Resposta

Não é segura.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma barra feita da liga de alumínio 2014-T6, seleciona a seção quadrada que pode ser usada, se a barra suporta uma carga centrada de 245 kN.

Duas cantoneiras de aço L102 x 76 x 9,5 são soldadas juntas para formar a coluna AB. Uma carga axial P, de intensidade 60 kN, é aplicada no ponto D. Usando o método da tensão admissível, determinar o

Uma carga de 15 kN é aplicada com uma excentricidade e = 0,2d a uma coluna quadrada de madeira com um comprimento efetivo de 3,5m. Para o tipo de madeira usada, E = 12,5 GPa e a tensão admissível à co

Um tubo estrutural com a seção transversal mostrada é usado como uma coluna para suportar uma carga centrada de 155 kN. Determinar o maior comprimento efetivo admissível do tubo, quando a liga de alum

Resolver o problema 116 assumindo que o comprimento efetivo da coluna é de: a) 3,6 mm e 1,2 m)