Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 106

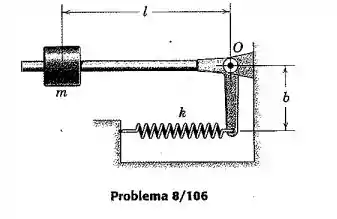
O comprimento da mola é ajustado de modo que a posição de equilíbrio do braço é horizontal conforme mostrado. Despreze a massa da mola e do braço e calcule a frequência natural f n para pequenas oscilações.

Passo 1

Para resolvermos esse problema, vamos usar as relações de torque resultante como também usaremos conservação de energia para encontrar a equação de oscilação para o sistema.

Passo 2

Vamos começar analisando as forças para o sistema em equilíbrio. Temos que no estado inicial, todas as forças estão em equilíbrio e não há torque resultante. Assim, temos que

τ = 0

F → e l a s t i c a + F → p e s o = 0

- k ⋅ Δ x ⋅ b ⋅ sin ⁡ 0 º - m ⋅ g ⋅ l ⋅ sin ⁡ 0 º = 0

Δ x = m ⋅ g ⋅ l k ⋅ b

Agora sabemos como se dá o deslocamento da mola. Podemos agora aplicar a conservação de energia para quando o sistema entra em movimento. Para o deslocamento, temos que quando a mola sai do equilíbrio teremos uma quantidade de deslocamento a mais causada pelo ângulo que será b ⋅ sin ⁡ θ . Temos então que

E = T + U

E = 1 2 ⋅ m ⋅ l ⋅ θ ˙ 2 + 1 2 ⋅ k ⋅ m ⋅ g ⋅ l k ⋅ b + b ⋅ sin ⁡ θ 2 - m ⋅ g ⋅ l ⋅ sin ⁡ θ

Se derivarmos a equação da energia mecânica, temos que d E d t = 0 . Assim, temos que

0 = d d t 1 2 ⋅ m ⋅ l ⋅ θ ˙ 2 + 1 2 ⋅ k ⋅ m ⋅ g ⋅ l k ⋅ b + b ⋅ sin ⁡ θ 2 - m ⋅ g ⋅ l ⋅ sin ⁡ θ

0 = m ⋅ l 2 ⋅ θ ¨ + k ⋅ m ⋅ g ⋅ l k ⋅ b + b ⋅ sin ⁡ θ ⋅ b ⋅ cos ⁡ θ ⋅ θ ˙ - m ⋅ g ⋅ l ⋅ cos ⁡ θ ⋅ θ ˙

0 = m ⋅ l 2 ⋅ θ ¨ + b 2 ⋅ k ⋅ sin ⁡ 2 ⋅ θ 2

Tomando θ ≈ 0 , temos que sin ⁡ 2 ⋅ θ ≈ 2 ⋅ θ . Assim, ficamos com

θ ¨ + k ⋅ b 2 m ⋅ l 2 ⋅ θ = 0

Temos então que nossa frequência angular natural será ω n = k ⋅ b 2 m ⋅ l 2 e temos que a frequência f n será

f n = ω n 2 ⋅ π = 1 2 ⋅ π ⋅ b l ⋅ k m

Resposta

f n = 1 2 ⋅ π ⋅ b l ⋅ k m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto de 1.50 kg oscila em uma mesa horizontal sem atrito presa na extremidade de uma mola com uma amplitude de 4.5 cm. Sua energia mecânica total é 1.4 J. Qual é a constante de força da mola?
Um objeto de 1.50 kg oscila em uma mesa horizontal sem atrito presa na extremidade de uma mola de constante de força k=500 N/m. A velocidade máxima do objeto é 70.0 cm/s. (a) qual é a energia mecânica
Um objeto de 2.4k g em uma superfície horizontal sem atrito é preso a uma das extremidades de uma mola horizontal de constante k = 4.5k N / m . A outra extremidade da mola é presa fixada. A mola é est
Um objeto de 3 kg oscila em uma mesa horizontal sem atrito presa na extremidade de uma mola de constante de força k=2.0 kN/m e uma energia mecânica total de 0.90 J (a) qual é a amplitude do movimento?
Um objeto de 3.00k g oscila em uma mesa horizontal sem atrito presa na extremidade de uma mola com uma amplitude de 8.0c m sua aceleração máxima é 3.5 m / s 2 . Encontre a energia mecânica total