Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 119
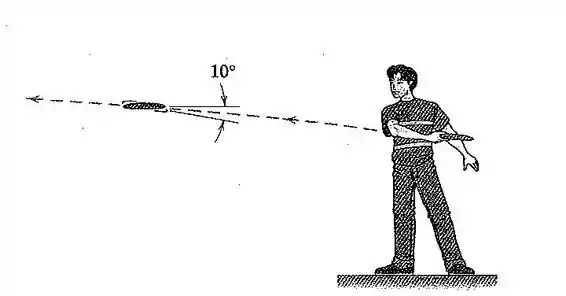
119. Um menino lança um disco circular fino (como um ) com uma velocidade de giro de . Observa-se o plano do disco oscilar através de um ângulo total de . Calcule o período da oscilação e indique se a precessão é direta ou retrógrada.
Passo 1
Bem! Essa questão é mais simples do que parece! Basta lembrar que a taxa precessional de oscilação é dada por:
Onde é o momento de inércia da estrutura em relação ao seu eixo geométrico perpendicular ao disco e o momento em relação ao eixo que passa pelo centro de massa, sendo paralelo ao disco:
E sabemos que os nossos momentos são:
Pelo que ficamos com:
E o nosso período da oscilação, sabemos que é dado por:
Por fim, como , a precessão vai ser retrógrada!
Resposta
Exercícios de Livros Relacionados
O disco circular está girando em torno do eixo OC com velocidade angular constante ω =20r a d / s . Em um determinado instante, o ponto A sobre a borda passa por um ponto cujas coordenadas x-y-z são 4
A barra é articulada em torno do eixo O-O do garfo, eu está preso à extremidade do eixo vertical. O eixo gira com uma velocidade angular constante ω 0 como mostrado. Se θ está diminuindo na taxa const
A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone
A haste vertical e o seu garfo vinculado giram em torno do eixo z na taxa constante Ω = 4r a d / s . Simultaneamente, a haste B gira em torno de seu eixo AO na taxa constante de w0 = 3 rad/s e o ângul
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . Determine a aceleração angular do haltere. O conjunto inteir