Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 1

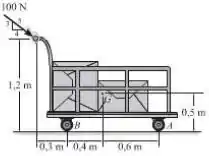
O carrinho e sua carga têm uma massa total de 100   k g . Determine a aceleração do carrinho e as reações normais sobre o par de rodas em A e B . Despreze a massa das rodas.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O exercício nos pede a aceleração do carrinho e as reações normais sobre o par de rodas em A e B .

Para determinar a aceleração do carrinho, podemos analisar o movimento horizontal:

→ + ∑ F x = m a G x

Fica mais fácil com um desenho né? Então vamos esboçar o diagrama de corpo livre:

A análise do desenho nos permite observar que a componente horizontal e vertical da força de 100   N valem, respectivamente:

F x = 100 4 5 = 80   N

F y = 100 3 5 = 60   N

Quando a força age no carrinho, ele começa a entrar em movimento tendo então uma aceleração em x provocada pela força horizontal.

Portanto:

→ + ∑ F x = m a G x

80 = 100 a

a = 0,8   m / s 2

Passo 2

Para determinar as reações, podemos fazer a análise dinâmica das forças verticais:

+ ↑ ∑ F y = m a G y

Sabemos que a aceleração do sistema no eixo y é nula, portanto:

N A + N B - 60 - 100 9,81 = 0

N A + N B = 1041

Passo 3

Agora faremos a análise do momento em G , considerando positivo o sentido anti-horário:

↶ ∑ M G = 0

N A 0,6 + 60 0,7 - N B 0,4 - 80 0,7 = 0

0,6 N A - 0,4 N B = 14

N A = 14 + 0,4 N B 0,6

Agora é só substituir na primeira equação encontrada:

14 + 0,4 N B 0,6 + N B = 1041

14 + 0,4 N B + 0,6 N B = 624,6

N B = 610,6   N

Logo:

N A = 14 + 0,4 ( 610,6 ) 0,6

N A = 430,4   N

Resposta

a = 0,8   m / s 2

N B = 610,6   N

N A = 430,4   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra de aço esbelta AB possui uma massa de 2.8 kg e está ligada ao eixo que gira pela barra OG e suas conexões em O e G. O ângulo β permanece constante em 30º, e todo o conjunto rígido gira em torn
O cilindro semicircular maciço de massa m gira em torno do eixo z como uma velocidade angular ω conforme indicado. Determine a sua quantidade de momento angular H em relação aos eixos x-y-z.
Cada uma das hastes esbeltas de comprimento l e massa m está soldada ao disco circular que gira em torno do eixo vertical z com uma velocidade angular ω . Cada haste faz um ângulo β com a vertical e e
O conjunto que consiste na esfera maciça de massa m e na barra uniforme de comprimento 2c e massa igual m, gira em torno do eixo vertical z com uma velocidade angular ω . A barra de comprimento 2c tem
Em um teste dos painéis solares para uma nava espacial, o modelo apresentado está girando em torno do eixo vertical na velocidade angular ω . Se a massa por unidade de área do painel é ρ , escreva a e