Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 142

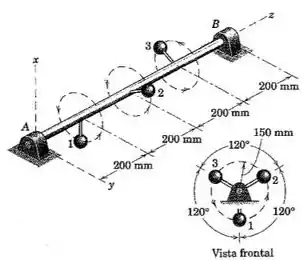
142. O desbalanceamento dinâmico de um determinado virabrequim é aproximado pela modelo físico apresentado, onde o eixo sustenta três esferas pequenas de 0,6   k g fixadas por hastes de massa desprezível. Se o eixo gira na velocidade constante de 1200   r p m , calcule as forças R A e R B que agem sobre os mancais. Despreze as forças gravitacionais.

Passo 1

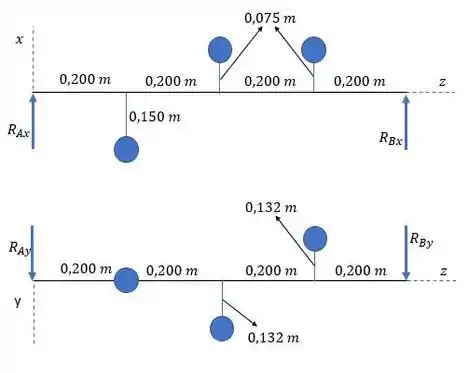
Bom, primeiro vamos esquematizar o sistema tanto no eixo x - z quanto no eixo y - z :

Passo 2

Agora, vamos transformar a velocidade angular que está em r p m e transformá-la em r a d / s :

ω z = ω   r p m 2 π 60

ω z = 1200   r p m 2 π 60

∴ ω z = 40 π   r a d / s

Passo 3

Como nós já temos as equações:

∑ M x = I y z ω z 2

∑ M y = - I x z ω z 2

Onde:

I y z = m ( 0,132   m × 0,400   m - 0,132   m × 0,600   m )

I y z = ( 0,600   k g ) ( 0,0528   m 2 - 0,0792   m 2 )

I y z = ( 0,600   k g ) ( - 0,0264   m 2 )

∴ I y z = - 0,01584   k g ⋅ m 2

I x z = m ( - 0,150   m × 0,200   m + 0,075   m × 0,400   m + 0,075   m × 0,600   m )

I x z = ( 0,600   k g ) ( - 0,030   m 2 + 0,030   m 2 + 0,045   m 2 )

I x z = ( 0,600   k g ) ( 0,045   m 2 )

∴ I x z = 0,027   k g ⋅ m 2

Passo 4

Se fizermos o somatório de momentos em relação ao eixo x :

∑ M x = - 0,800   m × R B y

E se igualarmos com o somatório do Passo anterior e substituir as variáveis, temos:

- 0,800 ⋅ R B y   N ⋅ m = ( - 0,01584   k g ⋅ m 2 ) ( 40 π   r a d / s ) 2

R B y = - 0,01584   k g ⋅ m 2 40 π r a d / s 2 - 0,800   m

R B y = ( - 0,01584   k g ⋅ m 2 ) ( 15791,37   r a d / s ) 2 - 0,800   m

R B y = 250,13   k g ⋅ m 2 / s 2 0,800   m

∴ R B y = 312,66   N

E fazendo o mesmo somatório em relação ao eixo y :

∑ M y = 0,800   m × R B x

E igualando o somatório do Passo anterior e subtituindo as variáveis, temos:

0,800 ⋅ R B x   N ⋅ m = - ( 0,027   k g ⋅ m 2 ) ( 40 π   r a d / s ) 2

R B x = - 0,027   k g ⋅ m 2 40 π r a d / s 2 0,800   m

R B x = - ( 0,027   k g ⋅ m 2 ) ( 15791,37   r a d / s ) 2 0,800   m

R B x = - 426,37   k g ⋅ m 2 / s 2 0,800   m

∴ R B x = - 532,96   N

Passo 5

Como o centro de massa não tem aceleração:

R A y = - R B y

R A x = R B x

E disso concluímos que:

R A = R B

R B = R B x 2 + R B y 2

R B = - 532,96   N 2 + 312,66   N 2

R B = 284046,3616   N 2 + 97756,2756   N 2

R B = 381802,6372   N 2

∴ R B = R A = 617,90   N

Resposta

As forças R A e R B que agem nos mancais são:

R B = R A = 617,90   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a aceleração máxima do caminhão sem fazer com que a montagem se desloque em relação ao caminhão. Além disso qual é a reação normal correspondente sobre as pernas A e B ? A mesa de 100k g tem
No instante mostrado, o membro C D gira com uma velocidade angular ω = 6r a d / s . Se ele está sujeito a um momento de binário M = 450N ⋅ m , determine a força desenvolvida no membro A B , a componen
Se o caminhão acelera a uma razão constante de 6m / s 2 , partindo do repouso, determine a aceleração angular inicial da escada de 20k g . A escada pode ser considerada como uma barra fina uniforme. O
Exercício de Livro
Exercício de Livro