A configuração mostrada é projetada para produzir a oscilação do recipiente de pequenas peças em torno de C, como parte de um processo de produção. Obtenha uma expressão para a aceleração angular do recipiente para a posição onde o elemento de ligação AB e a manivela AO estão na posição vertical com BC horizontal. A manivela está girando no sentido horário com uma velocidade angular constante durante um curto intervalo de movimento.

Olá pessoal! O enunciado mostra um mecanismo com a seguinte configuração.

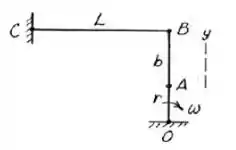
Primeiro, vamos calcular a velocidade angular e a aceleração do ponto A com os dados fornecidos.

Neste instante, o ponto A possui a componente de velocidade na direção vertical nula, pois sua velocidade é perpendicular à manivela AO. Como consequência da barra AB, o ponto B também possui velocidade nula nesta direção.

Porém, nesta condição mostrada no esquema, a componente de B na horizontal também é nula. Temos então:

Deste modo, o ponto B é o Centro Instantâneo da barra AB, podendo ser obtidas as relações:

Aplicando a equação da aceleração relativa nos pontos A e B, temos:

Arrumando a equação:

E por fim, igualamos o termo acima com a definição da aceleração tangencial: