Determine a aceleração do pistão do Exemplo 5/15 para (a) Considere o sentido positivo da direção x para a direita.
Passo 1
Primeiramente, vamos pegar alguns dados do Exemplo:
- Nesta condição:
- Nesta condição:
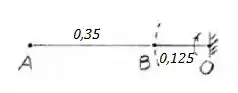
Passo 2
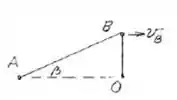
Portanto:
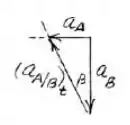
Passo 2
- Nesta condição:

Determine a aceleração do pistão do Exemplo 5/15 para (a) Considere o sentido positivo da direção x para a direita.
Primeiramente, vamos pegar alguns dados do Exemplo:
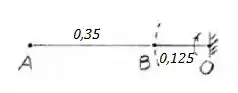

Portanto:

