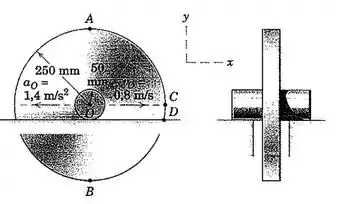
O conjunto eixo e roda do Prob. 5/102 é reapresentado aqui com a especificação adicional de que a aceleração do Centro O é de 1,4m / s 2 para a esquerda conforme mostrado. Se o eixo rola sobre a superfície horizontal fixa sem deslizar, determine as acelerações dos pontos A e D.

a D = - 62,7i ^ + 19,7j ^m / s 2

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 133

O conjunto eixo e roda do Prob. 5/102 é reapresentado aqui com a especificação adicional de que a aceleração do Centro O é de para a esquerda conforme mostrado. Se o eixo rola sobre a superfície horizontal fixa sem deslizar, determine as acelerações dos pontos A e D.

Passo 1

Este exercício reque alguns dados calculados no prob. 5/102, da seção anterior. Entretanto, não custa nada dar uma relembrada.

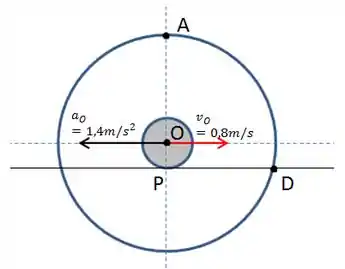
Exercícios de rolamento sem deslizamento quase sempre precisa de algumas equações derivadas do Centro Instantâneo de Velocidade nula para ajudar na resolução.

E este exercício não é diferente disso! Em rolamento sem deslizamento, sabemos que o Centro Instantâneo está localizado no ponto de contato entre a roda e o chão. Então, vale a relação:

Daí, tiramos que:

Passo 2

Sabendo a velocidade e a aceleração angular da roda, podemos calcular as velocidades e acelerações dos pontos A e D.

Para o ponto A, temos que:

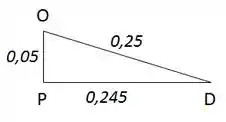
Faremos de forma análoga para o ponto D, porém pelo triângulo OPD, temos que o vetor posição

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.139. As rodas fixadas às extremidades da barra AB rolam ao longo das superfícies mostradas na figura. Usando o método da Seção 15.9 e sabendo que a aceleração da roda B é zero, deduza uma expressão

O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s2, ambas orientadas para ci

Um tambor de 75 mm de raio está preso rigidamente a um tambor de 125 mm de raio, como mostra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do

15.144. No instante mostrado na figura, a barra AB gira com uma velocidade angular constante ω e uma aceleração angular α , ambas no sentido horário. Usando o método da Seção 15.9, deduza expressões p