Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 116

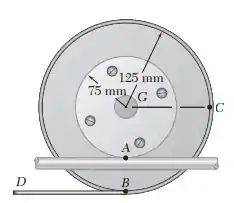
Um tambor de 75 mm de raio está preso rigidamente a um tambor de 125 mm de raio, como mostra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do outro tambor. Sabendo que, no instante mostrado, a extremidade D da corda tem velocidade de 200 mm/s e aceleração de 750 mm/s², ambas orientadas para a esquerda, determine as acelerações dos pontos A, B e C dos tambores.

Passo 1

Vamos lá resolver mais essa. A velocidade do ponto B, que está na mesma linha de ação do ponto D, tem a mesma velocidade de D, ou seja, v B = v D = 200   m m / s . Vamos assumir um centro de rotação no ponto A. Assim:

v B = A B ω → 200 = 125 - 75 ω

ω = 4   r a d / s   ( s e n t i d o   h o r á r i o )

Vamos assumir a aceleração angular do tambor tenha sentido horário. Avaliando a aceleração de A em relação a B, temos:

a → A = a → B + a → A / B t + a → A / B n

a A j → = - 750 i → + a A n j → - α k → × A B j → - ω 2 A B j → = - 750 i → + a A n j → + 50 α i → - 800 j →

Igualando as coordenadas de cada lado da equação:

0 = - 750 + 50 α → α = 15   r a d / s 2

Passo 2

Agora vamos avaliar a aceleração do ponto A em relação ao ponto G:

a → A = a → G + a → A / G t + a → A / G n

a A j → = a G i → - α k → × - G A j → - ω 2 - G A j → = a G i → - 1125 i → + 1200 j →

Igualando as coordenadas de cada lado da equação:

0 =   a G - 112 5 → a G = 1125   m m / s 2

a A = 1200   m m / s 2

De modo semelhante, avaliando a aceleração do ponto B em relação ao ponto G:

a → B = a → G + a → B / G t + a → B / G n

a → B = 1125 i → - 15 k → × - G B j → - ω 2 - G B j → = 1125 i → - 1875 i → + 200 0 j →

a → B =   - 750 i → + 200 0 j →

a B =   - 750 2 + 200 0 2 = 2136   m m / s 2

Passo 3

Avaliando a aceleração do ponto C em relação ao ponto G:

a → C = a → G + a → C / G t + a → C / G n

a → C = a G i → - 15 k → × G C i → - ω 2 G C i → = 112 5 i → - 1875 j → - 2000 i →

a → C =   - 875 i → - 1875 j →

a C =   - 875 2 + - 1875 2 = 2069,1   m m / s 2

Resposta

a A = 1200   m m / s 2   ; a B = 2136   m m / s 2   ; a C = 2069,1   m m / s 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.146. A posição da barra AB é controlada por um disco de raio r que está preso no balancim CD. Sabendo que o balancim se desloca verticalmente para cima com velocidade constante v0, deduza uma expre
15.147. No Problema 15.146, deduza uma expressão para a aceleração angular da barra AB.
15.145. No instante mostrado na figura, a barra AB gira com uma velocidade angular constante ω e uma aceleração angular α , ambas no sentido horário. Usando o método da Seção 15.9, deduza expressões p
15.148. Uma roda de raio r rola sem escorregar ao longo do interior de um cilindro fixo de raio R com uma velocidade angular constante . Representando por P o ponto da roda em contato com o cilindro e
15.149. No Problema 15.148, mostre que a trajetória de P é uma linha reta vertical quando r= R /2. Deduza expressões para a velocidade e aceleração de P correspondentes em qualquer instante t.