15.144. No instante mostrado na figura, a barra AB gira com uma velocidade angular constante e uma aceleração angular , ambas no sentido horário. Usando o método da Seção 15.9, deduza expressões para a velocidade e a aceleração do ponto C.
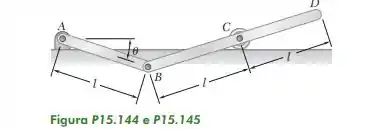
Passo 1
Vamos começar o exercício simplificando a imagem
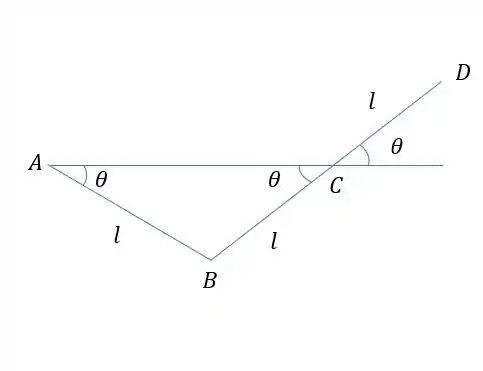
Vamos colocar a origem do sistema no ponto A. E ai ficamos com o seguinte
Passo 2
Agora vamos derivar isso
E
E a segunda derivada fica
E
Continua nulo.
Mas temos algumas informações importantes agora. Sabemos que
Também podemos perceber pela imagem que
E com o mesmo raciocínio
Passo 3
Agora podemos escrever as funções de velocidade
E
E da aceleração
E