Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 64
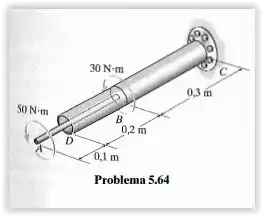
O conjunto é feito de aço A-36 e é composto por uma haste maciça de de diâmetro conectada ao interior de um tubo por meio de um disco rígido em . Determine o ângulo de torção em . O tubo tem diâmetro externo de e espessura de parede de .
Passo 1
Olá, pessoal! Tudo bem? Vamos analisar essa questão?
O problema pede que determinemos o ângulo de torção em .
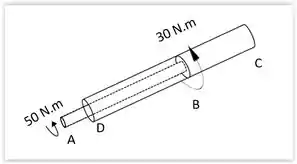
E para isso nos fornece:
Aço A-36, portanto,
Pode-se perceber pela imagem o ângulo na extremidade é influenciado pelo ângulo no cilindro entre e e na haste de até , mas não é influenciado pelo ângulo no tubo entre e por essa ser uma região sem contato direto com a haste que contém a extremidade . Sendo assim:
Passo 2
Vamos agora calcular os valores dos torques que provocaram a mudança de cada ângulo. A ideia aqui é a mesma que a gente fazia para achar esforços internos. A gente vai cortar nossas seções, colocar a componente do torque interno e achar seu valor pelo equilíbrio.
A começar pelo torque .
Por ser uma secção sem torques intermediários, o torque na extremidade é igual ao .
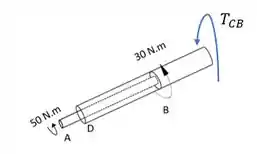
Já torque tem interferência do torque no ponto , que é somado ao torque por ambos serem no mesmo sentido. Para equilibrar, devemos ter
Passo 3
Com os torques determinados, nos resta apenas determinar os momentos polares de inércia e achar o valor do ângulo de torção.
A região é uma haste maciça de diâmetro igual a , logo,
A região é um tubo de diâmetro externo igual a e espessura de . Logo seu raio interno é :
Passo 4
O ângulo é dado por:
Sendo que:
Logo:
Convertendo para graus: