Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 14
A forma original de uma peça de plástico é retangular. Determine a deformação normal média que ocorrer ao longo das diagonais AC e DB.
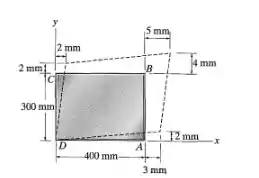
Passo 1
Vamos, primeiramente, representar a situação e nomear alguns ângulos:
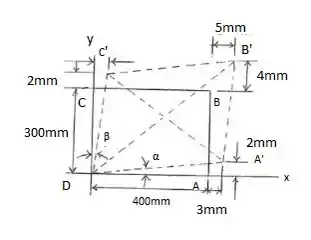
Por Pitágoras, podemos obter algumas relações:
Podemos também determinar os ângulos utilizando as relações trigonométricas:
-1
-1=
Passo 2
Vamos utilizar lei dos cossenos para determinar A’C’:
Passo 3
Com os comprimentos finais, podemos calcular as deformações na diagonais:
-3
-3
Resposta
-3
-3
Exercícios de Livros Relacionados
Mostre que, para o caso do estado plano de tensão, a lei de Hooke pode ser expressa como σ x = E 1 - y 2 ∈ x + v ∈ y , σ y = E 1 - y 2 ∈ y + v ∈ x
O eixo tem raio de 15 mm e é feito de aço-ferramenta L2. Determine as deformações nas direções x’ e y’, se for aplicado um torque T = 2 kN.m ao eixo.
Uma barra de liga de cobre é carregada em um equipamento de ensaio de tração e constata-se que ∈ x = 94 10 - 6 e σ x = 100 M P a , σ y = 0 ,σ z = 0 . Determine o módulo de elasticidade, E c u , e a di
A roseta de deformação a 60 ° está montada sobre uma viga. As seguintes leituras foram obtidas em cada extensômetro: ∈ a=150 × 10 - 6 , ∈ b = 330 × 10 - 6 , ∈ c = 400 × 10 - 6 . Determine (a) as defor
Um extensômetro colocado no plano vertical sobre a superfície externa a um ângulo de 60° em relação ao eixo do tubo dá uma leitura ∈ x = - 250 × 10 - 6 no ponto A. Determine a força vertical P, se o t