Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 68

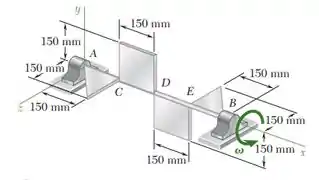
O conjunto mostrado na figura consiste de pedaços de chapa de alumínio de espessura uniforme e massa total de 2,] soldados a um eixoleve apoiado em mancais A e B. Sabendo que o conjunto gira a umataxa constante ω =   240 rpm, determine as reações dinâmicas em A e B.

∙

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente determine as reações dinâmicas em A e B

Massa da folha de metal: m = 2.7 32.2 = 0.08385   l b ∙ s 2 / f t

Dimensão da chapa metálica. b = 6   i n .   = 0.5   f t

Área de chapa metálica. A = 1 2 b 2 + b 2 + b 2 + 1 2 b 2 = 3 b 2 = 0.75   f t ²

Vamos ρ = m A = 0.08385 0.75 = 0.1118   l b ∙ s 2 / f t ³ = massa por unidade de área.

Momentos e produtos de inércia: I m a s s a = ρ I a r e a

x y   p l a n o   r e t â n g u l o

I x = 1 3 b 4 + 1 3 b 4 = 2 3 b 4

I x = 2 3   ρ b 4 = 2 3   ( 0.1118 ) ( 0.5 ) 4 = 4.658 × 10 - 3   l b ∙ s ² ∙ f t

I x y = b 2 3 2 b 1 2 b + b 2 5 2 b - 1 2 b = - 1 2 b 4

I x y = - 1 2   ρ b 4 = - 1 2   ( 0.1118 ) ( 0.5 ) 4 = - 3.4938 × 10 - 3   l b ∙ s ² ∙ f t

x y   p l a n o   t r i â n g u l o

I x = 1 12 b 4 + 1 12 b 4 = 1 6 b 4

I x = 1 6   ρ b 4 = 1 6   ( 0.1118 ) ( 0.5 ) 4 = 1.1646 × 10 - 3   l b ∙ s ² ∙ f t

Passo 2

Para o cálculo de I x z , use pares de elementos d A 1   e   d A 2 .

d A 2 =   d A 1

I x z = ∫ x z 2   d A 1 + ∫ 4 b - x - z 2 d A 2 = - ∫ 2 b - x z   d A 1 = - ∫ 0 b 2 b - x z 2   d x

Mas, z = x

Consequentemente, I x z = - ∫ 0 a 2 b x 2 - x 3 d x = - 2 3   b 4 - 1 4 b 4 = - 5 12   b 4

Total para I x : I x = 4.658 × 10 - 3 + 1.1646 × 10 - 3 = 5.823 × 10 - 3 l b ∙ s ² ∙ f t

O centro de massa encontra-se no eixo de rotação, portanto: a - = 0

∑ F = A + B = m a - = 0                     A = - B

H A = I x ω i - I x y ω j - I x z ω k                 ω = ω i                 α = α i

Deixe o quadro de referência A x y z ser rotático, com velocidade angular:

Ω = ω = ω i

]

∑ M A = H ˙ A = ( H ˙ A ) A x y z + Ω × H A

M 0 i + 4 b i × B y j + B z k = I x α i - I x y   α j - I x z α k + ω i × ( I x ω i - I x y ω j - I x z ω k )

M 0 i - 4 b B z j + 4 b B y k = I x α i - ( I x y   α - I x y ω ² ) j - ( (   I x z   α - I x y ω ² ) k

Passo 3

Resolva em componentes e resolva para B y   e   B z .

i :             M 0 = I x α

j :           B z = (   I x y   α - I x z ω ² ) 4 b

k :           B y = - (   I x y   α - I x y ω ² ) 4 b  

Dados: α = 0 ,           ω = 2 π   ( 240 ) 60 = 25.133   r a d / s ,           b = 0.5   f t         M 0 = 0

B z = 0 - ( - 2.9115 × 10 - 3 ) ( 25.133 ) ² ( 4 ) ( 0.5 ) = 0.91955   l b

B y = 0 + ( - 2.9115 × 10 - 3 ) ( 25.133 ) ² ( 4 ) ( 0.5 ) = 1.10346   l b

A y = - B y = - 1.10346   l b

A z = - B z = - 0.91955   l b

Resposta

a) A = - 1.103   l b j - 0.920   l b k

b) B =   1.103   l b j - 0.920   l b k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de aço com 3,6m possui uma massa de 125k g e é içada a partir do repouso onde a tração em cada um dos cabos é de 613N . Se o tambores de elevação recebem acelerações angulares iniciais α 1 = 4r
Determine a energia cinética perdida quando o canto C da placa do Problema 18.31 bate na obstrução.
Determine a energia cinética perdida quando a placa do Problema 18.29 bate na obstrução no ponto B.
Um eixo de 8 kg mostrado na figura tem uma seção transversal constante. Sabendo que o eixo gira com uma taxa constante ω = 12 rad /s, determine as reações dinâmicas nos pontos A e B.