Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 67
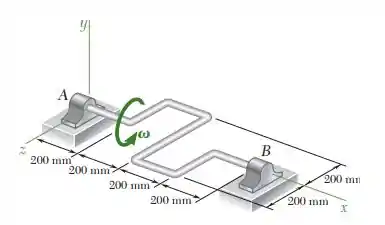
Um eixo de 8 kg mostrado na figura tem uma seção transversal constante. Sabendo que o eixo gira com uma taxa constante = 12 rad /s, determine as reações dinâmicas nos pontos A e B.
Passo 1
Vamos lá resolver mais essa. Temos que determinar as reações dinâmicas nos pontos A e B. Para isso, vamos determinar os momentos envolvidos no movimento. A velocidade angular é:
O momento angular sobre o centro de massa G é:
Vamos assumir que o eixo de referência rotacional com uma certa velocidade angular:
Assim, a taxa de variação é:
Como o eixo está localizado no plano xz,
Passo 2
Agora vamos determinar as forças e os momentos de inércia. Por simetria, o centro de massa está localizado na linha AB. No centro de massa, a aceleração é nula. Assim,
As forças A e B funcionam com um binário. Fazendo o somatório dos momentos no centro de massa, temos:
em que b é a distância entre o ponto A e B e
Para os cálculos do momento de inércia, vamos separar o eixo em 8 segmentos, como mostra a figura abaixo
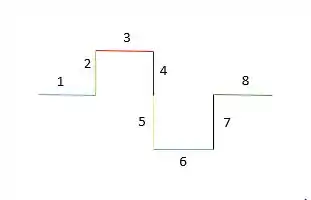
A massa de cada segmento é:
Para os segmentos 1, 4, 5 e 8,
Com isso,
Passo 3
Agora, a gente substitui os valores do momento de inércia e de velocidade angular na equação de :
Como , temos:
Assim,