Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 92
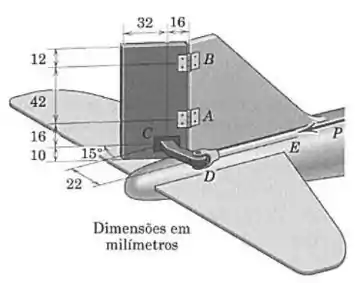
Considere o conjunto do leme de um aeromodelo controlado por rádio. Para a posição a mostrada na figura, a pressão atuando no lado esquerdo da área retangular do leme vale . Determine a força necessária na barra de controle e as componentes horizontais das reações nas dobradiças e , que são paralelas à superfície do leme. Considere a pressão aerodinâmica como sendo uniforme.
Passo 1
Como a pressão aerodinâmica é uniforme, podemos tratar a força associada a ela como se estivesse agindo no centro da placa, e calcular seu módulo da seguinte forma:
Além dessa força agindo no centro da placa, temos as componentes , , , , e nas dobradiças e a força na barra de sustentação.
Vamos escrever algumas equações de equilíbrio com o objetivo de encontar os valores de , e .
Passo 2
Começamos com o momento em relação ao eixo , porque nesse caso vamos excluir todas as forças nas dobradiças, e sobram apenas e .
A distância da força até o eixo segue a seguinte expressão (dê uma olhada na figura para entender isso):
E favoree a rotação no sentido horário em relação ao eixo . Já a força está a do eixo , e favorece a rotação no sentido anti-horário, então:
Passo 3
Em seguida vamos olhar para o momento em relação à linha de ação da força , porque nesse caso excluiremos todas as forças que agem em , além das forças e (que são paralelas a ) , e a força , cuja linha de ação cruza a da força . Então:
A força está a da força , e a componente de que é perpendicular à linha está a . Além disso, as duas forças favorecem a rotação em sentidos contrários:
Passo 4
Agora vamos praticamente repetir o que fizemos no passo , mas em relação ao eixo da força , e dessa vez vamos encontrar .
Nem precisamos pensar muito, é só fazer uma equação “simétrica” à do passo anterior:
Resposta
As forças são , e .