Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 87
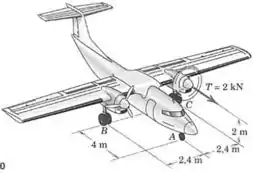
Durante um teste, o motor esquerdo de um avião bimotor é acionado gerando um empuxo de . As rodas principais em e estão freadas de modo a evitar movimento. Determine a variação nas forças de reação normais em , e (comparativamente aos valores nominais com ambos os motores desligados).
Passo 1
A ideia aqui é que o avião permaneça em equilíbrio quando o motor for ligado, e nosso objetivo é encontrar as variações , e nas forças normais de reação em , e que tornam isso possível.
Que outras forças estão atuando no sistema? Estamos pensando apenas nas forças que surgem depois que o motor é acionado (porque nosso interesse é na variação), então temos apenas as variações das normais e o empuxo gerado pelo motor:
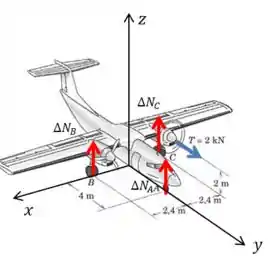
Já que temos três variáveis desconhecidas, precisamos procurar ao menos três equações de equilíbrio.
Perceba também que nós escolhemos a origem de forma que as distâncias dela até as forças sejam fáceis de escrever. Isso vai ficar mais claro logo em seguida.
Passo 2
Começamos pelo equilíbrio das forças na direção normal ao chão:
Essa é nossa primeira equação. Agora vamos pensar no equilíbrio dos momentos.
Começamos com o momento em relação ao eixo . As forças e cruzam o eixo, então não produzem nenhum momento nesse caso:
E o sinal negativo aparece antes do momento da força de porque ela favorece a rotação no sentido horário.
Vamos agora ao momento em relação ao eixo :
E nesse caso a força cruza o eixo e é paralela a ele, por isso essas duas forças não produzem momento.
Passo 3
Agora vamos juntar todas essas informações em um sistema:
Substituindo a segunda e a terceira equações na primeira:
E então a solução é:
Resposta
As variações nas forças são , .