Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 26
6/26) Calcule a força necessária para girar o carretel de cabo telefônico de , que se apoia em seu eixo e está enconstado contra uma parede vertical. O coeficiente de atrito dinâmico para cada par de superfícies em contato é .
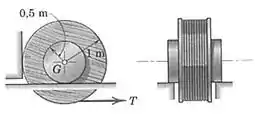
Passo 1
Bom pessoal , como de costume , para resolvermos este exercício aplicaremos as equações de equilíbrio que conhecemos (em relação aos eixos e e em relação ao momento ) .
Sendo assim , temos que :
Combinando as três equações e resolvendo o sistema linear associado a elas , achamos que :
Resposta
E aí , Topam resolver mais questões com a gente ?
Exercícios de Livros Relacionados
Se a garota com 35k g estiver na posição d = 1,2m , determine o coeficiente mínimo de atrito estático μ s nos pontos de contato A e B de modo que a tábua não deslize. Despreze o peso da tábua.
Se o coeficiente de atrito estático nos pontos de contato A e B é μ s = 0,4 , determine a distância mínima d onde uma garota de 35k g pode permanecer sobre a tábua sem que a tábua deslize. Despreze o
Se os coeficientes de atrito estático nos pontos de contato A e B são μ s = 0 , 3 e μ s ' = 0 , 4 , respectivamente, determine a menor força P que fará com que o carrretel de 150k g tenha iminência de
Se o coeficiente de atrito estático entre os colares A e B e a barra é μ s = 0,6 , determine o ângulo máximo θ para o sistema permanecer em equilíbrio, independente do peso do cilindro D . As ligações
Cada um dos cilindros tem uma massa de 50k g . Se os coeficientes de atrito estático nos pontos de contato são μ A = 0,5 , μ B = 0,5 , μ C = 0,5 e μ D = 0,6 , determie o menor momento de binário M nec