Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 20
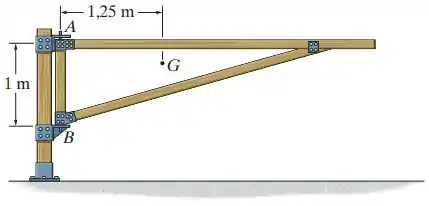
A porteira de 75 kg tem um centro de massa localizado em . Se apoia apenas uma força horizontal e pode ser considerado como um pino, determine as componentes das reações nesses apoios.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar as reações nos apoios e . Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!!
Sempre que tiverem dúvida, voltem na Tabela 5.1 do livro! Lá são identificados os tipos de apoios com as suas reações!
Como o apoio foi identificado como pino, significa que ele tem forças verticais e horizontais! Então, o nosso diagrama de forças será:
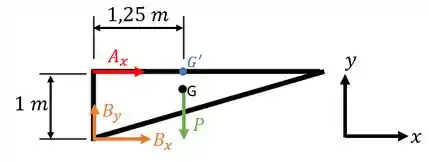
A parte chave desta questão é o ponto , projeção do ponto sobre o segmento horizontal que passa por . Percebam que o ponto dista um comprimento qualquer do segmento horizontal que passa por e qualquer do segmento horizontal que passa por !
Para que calculássemos o momento em torno do ponto , seria necessário sabermos estas distâncias e . Agora, quando formos calcular em relação ao ponto , isto não será mais necessário!
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Nosso trabalho agora é aplicar as relações de equilíbrio. Vamos começar pela identificação das forças!
Fazendo um somatório das forças na direção , temos:
E assim identificamos a nossa primeira reação!
Já para o somatório na direção , temos:
E acabamos sem concluir nada! Precisamos de outra equação para poder montar um sistema, e obter o valor das nossas duas incógnitas!
Passo 3
Para montarmos o sistema e finalizarmos a questão, vamos trabalhar com o somatório dos momentos! Fazendo em torno do ponto , temos:
E consequentemente,
E assim finalizamos a questão!