Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 53
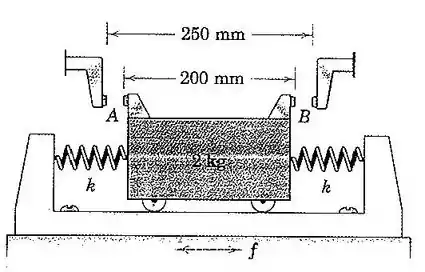
53. O corpo de está fixado a duas molas cada uma das quais com uma rigidez de . O corpo está montado sobre uma mesa vibratória que oscila harmonicamente na direção horizontal com uma amplitude de e uma frequência que pode ser variada. O fornecimento de energia elétrica para a mesa vibratória é desligado quando o contato elétrico é feito em ou . Determine o valor máximo da frequência em que a mesa vibratória pode ser operada sem desligar o aparelho, quando ele parte do repouso e aumenta sua frequência gradualmente. O amortecimento pode ser desprezado. A posição de equilíbrio é centralizada entre os contatos fixos.
Passo 1
Bom! Primeiramente vamos tratar de obter a frequência natural do nosso sistema, que é dada pela fórmula abaixo:
Multiplicamos por , porque o sistema está fixado por duas molas dada uma com sua rigidez . Agora, vamos tratar de substituir os valores numéricos pertinentes na nossa formulinha acima:
Passo 2
Em seguida, borá aplicar a fórmula da amplitude em regime permanente para uma oscilação harmônica da base:
E olhando a questão tiramos que o valor de é igual a .
Além disso, analisando a figura do enunciado, também podemos obter o valor da nossa amplitude , que é dada por:
Com isso temos tudo que precisamos para encontrar a frequência da nossa oscilação. Vamos então, substituir os valores que já conhecemos, na fórmula do :
Passo 3
Como já obtemos nossa frequência angular , basta lembrar que ela está relacionada com a frequência de acordo com a seguinte fórmula:
É só substituir que encontramos nossa resposta. Vamos lá!