Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 126

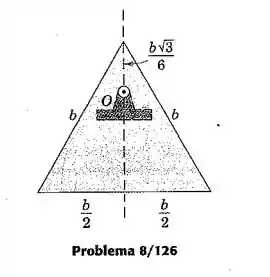
A placa triangular uniforme gira livremente em torno de um eixo horizontal que atravessa o ponto O . Determine a frequência natural para pequenas oscilações.

Passo 1

Para esse problema vamos usar as relações de torque resultante e de momento de inércia para descobrirmos a frequência de oscilação para pequenos ângulos.

Passo 2

Temos pela tabela D/3 que o momento de inércia parcial da placa triangular é

I X = 1 12 ⋅ b ⋅ h 3 = 1 12 ⋅ b ⋅ b ⋅ 3 2 3 = 3 32 ⋅ b 4

Mas temos que o momento de inércia no eixo x ' será dado por

I X ' X ' = I X ⋅ ρ = 3 32 ⋅ b 4 ⋅ 4 ⋅ m b 2 ⋅ 3 = 1 8 ⋅ m ⋅ b 2

Onde ρ é nossa densidade superficial que é dado por ρ = m A . Agora para y faremos o mesmo processo

I Y = 3 96 ⋅ b 4

I Y Y = I y ⋅ ρ = 3 96 ⋅ b 4 ⋅ 4 ⋅ m b 2 ⋅ 3 = 1 24 ⋅ m ⋅ b 2

Agora precisamos do momento de inércia total do sistema. Ele será dado pela soma dos momentos de inércia para cada eixo. Logo, temos que

I o = I X ' X ' + I Y Y = 1 8 ⋅ m ⋅ b 2 + 1 24 ⋅ m ⋅ b 2 = 1 6 ⋅ m ⋅ b 2

Aplicando agora o torque resultante, temos que a única força atuante no sistema será a força peso, dada por m ⋅ g ⋅ r O . Assim, temos que nosso torque será

Τ r = I o ⋅ θ ¨

- m ⋅ g ⋅ b ⋅ 3 6 ⋅ sin ⁡ θ = 1 6 ⋅ m ⋅ b 2 ⋅ θ ¨

θ ¨ + g ⋅ 3 b ⋅ sin ⁡ θ = 0

Usando agora θ para pequenas oscilações, temos que sin ⁡ θ → θ . Assim

θ ¨   + g ⋅ 3 b ⋅ θ = 0

ω n = g ⋅ 3 b

Resposta

ω n = g ⋅ 3 b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja r a razão entre dois máximos consecutivos do deslocamento de um oscilador livre fracamente amortecido ( γ ≪ ω 0 ). O parâmeto δ = ln ⁡ r chama-se decremento logarítmico. (a) Relacione δ com a con
Verifique que x 1 t = t e - γ 2 t é solução da x ¨ + γ x ˙ + ω 0 2 x = 0 para ω 0 = γ / 2 , e que a x t = F 0 2 m ω 0 t sen ⁡ ω 0 t satisfaz a equação diferencial x ¨ + ω 0 2 x = F 0 m cos ⁡ ω 0 t e a
Um bloco cúbico de 10c m de aresta e densidade 8g / c m 3 está suspenso do teto por uma mola de constante elástica 40N / m e comprimento relaxado de 0,5m , e mergulhado dentro de um fluido viscoso de
Uma partícula de massa m move-se na direção z no interior de um fluido, cuja resistência de atrito é da forma - ρ z ˙ ou seja, é proporcional à velocidade ρ0 . A força peso é desprezível em confronto
Um oscilador não amortecido de massa m e frequência própria ω 0 move-se sob a ação de uma força externa F = F 0 sen ⁡ ω t , partindo da posição de equilíbrio com velocidade inicial nula. Ache o desloc