Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 98

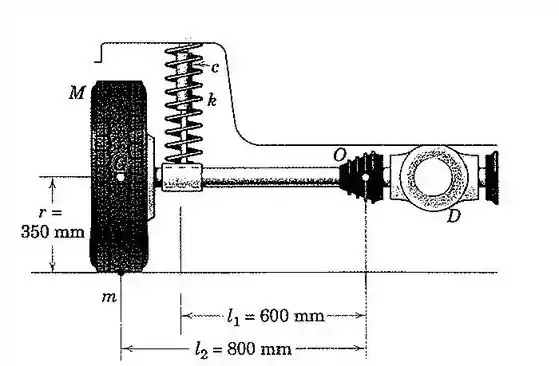
98. Para o sistema de suspensão do automóvel do Prob. 8 / 97 , determine a amplitude X do movimento vertical do ponto G , se a velocidade angular do pneu corresponde:

(a) à frequência natural não amortecida do sistema e

(b) a uma velocidade do veículo 90   k m / h . Compare os dois resultados.

Passo 1

Primeiro, vamos montar o diagrama de forças e momentos para a haste com a roda:

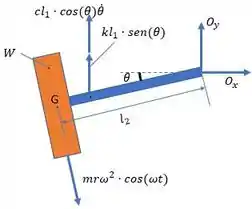
Passo 2

Agora, vamos calcular o momento de inércia do sistema em relação ao ponto O usando o teorema dos eixos paralelos:

I 0 = I G + m t l 2 2

I 0 = 1,4   k g ⋅ m 2 + 45,25   k g ⋅ 0,800   m 2

I 0 = 1,4   k g ⋅ m 2 + 28,96   k g ⋅ m 2

I 0 = 30,36   k g ⋅ m 2  

Passo 3

Depois bora tratar de fazer a soma de momentos em relação ao ponto O :

∑ M O = I 0 θ ¨

M 1 = - k l 1 ⋅ s e n θ l 1 ⋅ cos ⁡ θ

M 2 = - ( c l 1 θ ˙ ⋅ cos ⁡ θ ) ( l 1 ⋅ cos ⁡ θ )

M 3 = m r ω 2 ⋅ cos ⁡ ω t ⋅ c o s ⁡ ( θ ) l 2

M 1 + M 2 + M 3 = I 0 θ ¨

Para θ pequeno, temos s e n ( θ ) ≅ θ e c o s ⁡ ( θ ) ≅ 1

- k l 1 2 θ - c l 1 2 θ ˙ + l 2 m r ω 2 ⋅ cos ⁡ ω t = I 0 θ ¨

Rearranjando a equação:

θ ¨ + c l 1 2 I 0 θ ˙ + k l 1 2 I 0 θ = l 2 m r ω 2 ⋅ cos ⁡ ω t I 0

Passo 4

A solução particular da equação diferencial encontrada é:

θ = H ⋅ c o s ⁡ ( ω t - ϕ )

Sendo H a solução homogênea:

H = M 0 k t M = m r ω 2 l 2 k l 1 2 M

Se substituirmos M que é o fator amplificação, o qual é dado por:

M = 1 1 - ω ω n 2 2 + 2 ζ ω ω n 2 1 / 2

Obteremos então, a seguinte equação:

H = m r ω 2 l 2 k l 1 2 ⋅ 1 1 - ω ω n 2 2 + 2 ζ ω ω n 2 1 / 2

H = m r ω 2 l 2 / k l 1 2 1 - ω ω n 2 2 + 2 ζ ω ω n 2

Passo 5

Pra achar o fator de amortecimento ζ , vamos utilizar a relação:

2 ζ ω n = γ

2 ζ ω n = c l 1 2 I 0

ζ = c l 1 2 2 I 0 ω n

ζ = ( 2600   N ⋅ s / m ) ( 0,600   m ) 2 2 ( 30,36   k g ⋅ m 2 ) ( 10,18   r a d / s )

ζ = 2,52

Passo 6

(a) Para resolver esse item, vamos primeiramente calcular a frequência natural ω n :

ω n = k l 1 2 I 0 = ( 8,75   k N / m   ) ( 0,600   m ) 2 30,36   k g ⋅ m 2

ω n = 3150   N ⋅ m 30,36   k g ⋅ m 2

ω n = 103,75

ω n = 10,18   r a d / s

Passo 7

Porém, a frequência ω será a mesma frequência que ω n , pois ela é não amortecida:

ω ω n = 10,24   r a d / s 10,24   r a d / s = 1

Depois, substituindo nossos resultados anteriores em H , obtemos que:

H = ( 45,25   k g ) ( 0,350   m ) 10,24 r a d s 2 ( 0,800 m ) / ( 8,75   k N / m ) ( 0,600   m ) 2 1 - 1 2 2 + 2 ( 2,52 ) 1 2

H = 1328,55 / 3150 25,4016

H = 0,421 5,04

H ≅ 8,37 × 10 - 2   r a d

Passo 8

E o movimento vertical X é dado por:

X = l 2 H = ( 0,800   m ) ( 8,37 × 10 - 2   r a d )

X ≅ 6,69 × 10 - 2   m ≅ 6,69   c m

Passo 9

(b) Como temos a velocidade tangencial v , vamos calcular a velocidade angular ω pela fórmula:

ω = v r

Lembrando é claro de mudar a unidade da velocidade de k m / h para m / s :

ω = 90 3,6   m / s 0,350   m

ω = 71,43   r a d / s

Passo 10

E em seguida, calcularemos a razão:

ω ω n = 71,43   r a d / s 10,18   r a d / s = 7,017

E substituiremos na expressão de H lá do P a s s o   4 :

H = ( 45,25   k g ) ( 0,350   m ) 10,24 r a d s 2 ( 0,800 m ) / ( 8,75   k N / m ) ( 0,600   m ) 2 1 - 7,017 2 2 + 2 ( 2,52 ) ( 7,017 ) 2

H = 1328,55 / 3150 2326,52 + 1250,73

H = 0,421 3577,25

H = 0,421 59,81

H ≅ 0,00703   r a d ≅ 7,03 × 10 - 3   r a d

Passo 11

Para o movimento vertical X , temos então que:

X = l 2 H = ( 0,800   m ) ( 7,03 × 10 - 3   r a d )

X = 5,624 × 10 - 2   m = 5,624   c m

Resposta

(a) A amplitude do movimento vertical será:

X ≅ 6,69 × 10 - 2   m ≅ 6,69   c m

(b) A amplitude do movimento vertical será:

X ≅ 5,624 × 10 - 2   m ≅ 5,624   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema do Prob. 8/45 é repetido aqui. Se o elemento de ligação A B possui agora uma masssa m 3 e um raio de giração k O em relação ao ponto O , determine a equação do movimento em termos da variáve
Determine a frequência natural f n para pequenas oscilações do corpo composto no plano vertical em torno do mancal O . Aproxime o corpo como uma barra esbelta de massa m / 5 e um disco semicircular de
O disco circular de massa m e momento de inércia I , em relação a seu eixo central, está soldado ao eixo de aço, que, por sua vez, está soldado ao bloco fixo. O disco recebe um deslocamento angular θ
A polia cilíndriva, maciça e homogênea possui uma massa m 1 e um raio r . Se a peça em B é submetida ao deslocamento harmônico indicado, determine a equação de movimento do sistema em termos da variáv
Duas barras uniformes e idênticas estão soldadas uma à outra em um ângulo reto e são articuladas em relação a um eixo horizontal que atravessa o ponto O como mostrado. Determine a frequência de excita