Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 107
Uma partícula se desloca ao longo da trajetória curva mostrada. A partícula tem uma velocidade no instante e uma velocidade no instante . Determine os valores médios das acelerações normal e tangencial da partícula entre os pontos e .
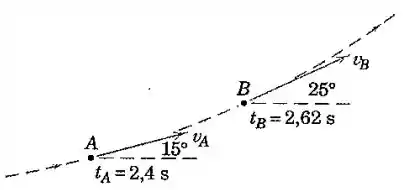
Passo 1
Pessoal, pra gente conseguir calcular a aceleração normal média , lembre-se que uma das fórmulas da aceleração normal é:
onde é a taxa de variação do ângulo em radianos por segundo. Então podemos obter desse modo:
onde é a velocidade média. Ou seja,
Lembre-se que temos que converter graus para radianos:
Passo 2
Agora, para calcular a aceleração tangencial média , lembre-se que a aceleração tangencial é dada por:
onde é a taxa de variação da velocidade. Então podemos obter desse modo:
Resposta
Exercícios de Livros Relacionados
Uma partícula P se desloca na trajetória circular mostrada. Desenhe o vetor aceleração a e determine o seu módulo a para os seguintes casos:(a) a velocidade v é 1,2m / s e é constante,(b) a velocidade
2/165) Para as condições do Prob. 2/164 , determine θ ' como uma função do tempo .
O foguete lançado verticalmente e o radar de rastreamento do Prob. 2/147 são apresentados aqui novamente. No instante em que θ = 60 ° , as medidas fornecem θ ˙ = 0,03r a d / s e r = 7500m , e a aceler
O deslocamento angular da centrífuga é dado por θ = 4 t + 30 e - 0,03 t - 30r a d , onde t é expresso em segundos e t = 0 é o instante da partida. Se o ser humano perde a consciência em um nível de ac
2/168) Uma cápsula P de fogos de artifício lançada em uma trajetóra vertical tem uma aceleração y dada por a y = - g - k v 2 , onde o último termo é devido ao arrasto aerodinâmico . Se a velocidade da