Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 33

O corpo quadrado homogêneo é posicionado conforme mostrado. Se o coeficiente de atrito estático em B for 0,40, determine o valor crítico do ângulo θ abaixo do qual ocorrerá o escorregamento. Negligencie o atrito em A.

Passo 1

Primeiro, vamos desenhar o diagrama de corpo livre de um quadrado

Uma vez que estamos procurando o valor crítico do ângulo θ, isso significa que a força de atrito é FB máximo

F B = μ s ⋅ N B F B = 0.40 N B                                                                                       ( 1 )

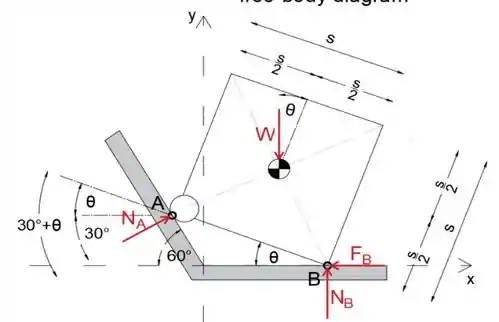
Equacionando a soma dos momentos sobre o ponto B a zero, determinaremos a força de reação normal à distância NA

∑ M B = 0

N A s i n ⁡ 30 ∘ + θ s - W c o s ⁡ θ s 2 + W s i n ⁡ θ s 2 = 0 N A = W ( c o s ⁡ θ - s i n ⁡ θ ) s 2 s i n ⁡ 30 ∘ + θ s N A = W cos ⁡ θ - sin ⁡ θ 2 sin ⁡ 30 ∘ + θ                                                                                                                         ( 2 )

Ao igualar a soma das forças nas direções x - e y - a zero, podemos escrever as forças FB e NB como função de NA

∑ F x = 0

N A c o s ⁡ 30 ∘ - F B = 0 F B = N A c o s ⁡ 30 ∘ F B = 0.866 N A

Substituiremos FB na expressão (1)

0.40 N B = 0.866 N A N B = 0.866 0.40 N A N B = 2.165 N A                                                                                                                                                     ( 3 )

∑ F y = 0

N A s i n ⁡ 30 ∘ - W + N B = 0 N B = W - N A s i n ⁡ 30 ∘ N B = W - 0.5 N A                                                                                                                                   ( 4 )

Passo 2

Vamos substituir NB na equação (4) pela expressão (3)

2.165 N A = W - 0.5 N A W = 2.665 N A

Substituiremos NA pela expressão (2)

W = 2.665 W ( c o s ⁡ θ - s i n ⁡ θ ) 2 s i n ⁡ 30 ∘ + θ W = 1.332 W ( c o s ⁡ θ - s i n ⁡ θ ) sin ⁡ 30 ∘ + θ s i n ⁡ 30 ∘ + θ = 1.332 ( c o s ⁡ θ - s i n ⁡ θ )

Substituiremos s i n ⁡ 30 ∘ + θ  por  s i n ⁡ 30 ∘ c o s ⁡ θ + s i n ⁡ θ c o s ⁡ 30 ∘

s i n ⁡ 30 ∘ c o s ⁡ θ + s i n ⁡ θ c o s ⁡ 30 ∘ = 1.332 c o s ⁡ θ - 1.332 s i n ⁡ θ 0.5 c o s ⁡ θ + 0.866 s i n ⁡ θ = 1.332 c o s ⁡ θ - 1.332 s i n ⁡ θ 2.198 s i n ⁡ θ = 0.832 c o s ⁡ θ t a n ⁡ θ = - 0.832 2.198 θ = t a n - 1 ⁡ 0.832 2.198

θ = 20.73 ∘

Resposta

θ = 20.73 ∘

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um rolo de papel tem um peso uniforme de 3,75N ( ≈ 0,375k g ) e está suspenso pela porta-papel de modo que se apoia contra a parede. Se o porta-papel tem um peso desprezível e o rolamento em O pode se
A garra é usada para apertar a conexão entre dois tubos de esgoto de concreto. Determine o menor coeficiente de atrito estático em A ou B de modo que a garra não deslize, independente da força no eixo
Se o coeficiente de atrito estático entre a corrente e o plano inclinado é μ = tan ⁡ θ , determine o comprimento pendurado b de modo que a corrente esteja prestes a deslizar plano acima. A corrente pe
Se θ = 30 º º, determine o menor coeficiente de atrito estático entre A e B de modo que o rolete permaneça preso, independente da intensidade da força P aplicada à correia. Despreze o peso do cilindro
Se o coeficiente de atrito estático em B é μ s = 0,3 , determine o maior ângulo θ e o menor coeficiente de atrito estático em A de modo que o cilindro permaneça preso, independente da intensidade da f